题目内容
14. 如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BD•cos∠HBD的值.
如图,在△ABC中,∠ABC=90°,BC=3,D为AC延长线上一点,AC=3CD,过点D作DH∥AB,交BC的延长线于点H,求BD•cos∠HBD的值.
分析 由DH与AB平行,得到一对内错角相等,再由一对内错角相等,利用两角相等的三角形相似得到三角形ABC与三角形DHC相似,由相似得比例求出CH的长,由BC+CH求出BH的长,在直角三角形BHD中,利用锐角三角函数定义求出所求式子的值即可.
解答 解:∵DH∥AB,
∴∠BHD=∠ABC=90°,
∵∠ACB=∠DCH,
∴△ABC∽△DHC,
∵AC=3CD,即$\frac{AC}{DC}$=$\frac{1}{3}$,
∴$\frac{AC}{DC}$=$\frac{BC}{HC}$=$\frac{1}{3}$,
又BC=3,
∴CH=1,
∴BH=BC+CH=3+1=4,
在Rt△BHD中,cos∠HBD=$\frac{BH}{BD}$,
∴BDcos∠HBD=BH=4.
点评 此题考查了相似三角形的判定与性质,以及解直角三角形,熟练掌握相似三角形的判定与性质是解本题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
5.下列计算中,正确的是( )
| A. | 3$\sqrt{3}$×3$\sqrt{2}$=3$\sqrt{6}$ | B. | $\sqrt{27}$÷$\sqrt{3}$=3 | C. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | D. | $\sqrt{(-7)^{2}}$=-7 |
12.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.

(1)根据图中提供的信息填表:
则S=$\frac{1}{2}$m+n-1(用含m、n的代数式表示)
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).


(1)根据图中提供的信息填表:
| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |
(2)对正三角形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,如图1、2是该正三角形格点中的两个多边形:设格点多边形的面积为S,该多边形各边上的格点个数之和为m,内部的格点个数为n,试探究S与m、n之间的关系式.则S与m、n之间的关系为S=m+2(n-1)(用含m、n的代数式表示).






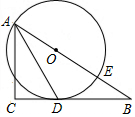 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).
二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号). 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.