题目内容
15.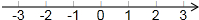 解不等式组$\left\{\begin{array}{l}{x+3≤5①}\\{2x+1>3(2-x)②}\end{array}\right.$.
解不等式组$\left\{\begin{array}{l}{x+3≤5①}\\{2x+1>3(2-x)②}\end{array}\right.$.(Ⅰ)解不等式①,得x≤2;
(Ⅱ)解不等式②,得x>1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为1<x≤2.
分析 先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可.
解答  解:$\left\{\begin{array}{l}{x+3≤5①}\\{2x+1>3(2-x)②}\end{array}\right.$.
解:$\left\{\begin{array}{l}{x+3≤5①}\\{2x+1>3(2-x)②}\end{array}\right.$.
(Ⅰ)解不等式①,得 x≤2;
(Ⅱ)解不等式②,得 x>1;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
(Ⅳ)原不等式组的解集为 1<x≤2.
故答案为x≤2,x>1,1<x≤2.
点评 本题考查了解一元一次不等式组,在数轴上表示不等式组的解集的应用,解此题的关键是能根据不等式的解集找出不等式组的解集,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.某校八年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个),经统计发现两班总分相等,此时有学生建议,可通过考查数据中的其他信息作为参考,请你回答下列问题:
(1)根据上表提供的数据填写下表:
(2)根据以上信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
友情提示:一组数据的方差计算公式是S2=$\frac{1}{n}$[(x1-x)2+(x2-x)2+…+(xn-x)2],其中$\overline{x}$为n个数据x1,x2,…,xn的平均数.
| 1号 | 2号 | 3号 | 4号 | 5号 | 总分 | |
| 甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
| 乙班 | 86 | 100 | 98 | 119 | 97 | 500 |
| 优秀率 | 中位数 | 方差 | |
| 甲班 | 60% | 100 | 46.8 |
| 乙班 | 40% | 98 | 114 |
友情提示:一组数据的方差计算公式是S2=$\frac{1}{n}$[(x1-x)2+(x2-x)2+…+(xn-x)2],其中$\overline{x}$为n个数据x1,x2,…,xn的平均数.
 已知AB=DE,BC=EF,D,C在AF上,且AD=CF,求证:AB∥DE.
已知AB=DE,BC=EF,D,C在AF上,且AD=CF,求证:AB∥DE.