题目内容
19.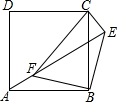 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.(1)求证:△ABF≌△CBE;
(2)判断△CEF的形状,并说明理由.
分析 (1)由四边形ABCD是正方形可得出AB=CB,∠ABC=90°,再由△EBF是等腰直角三角形可得出BE=BF,通过角的计算可得出∠ABF=∠CBE,利用全等三角形的判定定理SAS即可证出△ABF≌△CBE;
(2)根据△EBF是等腰直角三角形可得出∠BFE=∠FEB,通过角的计算可得出∠AFB=135°,再根据全等三角形的性质可得出∠CEB=∠AFB=135°,通过角的计算即可得出∠CEF=90°,从而得出△CEF是直角三角形.
解答 (1)证明:∵四边形ABCD是正方形,
∴AB=CB,∠ABC=90°,
∵△EBF是等腰直角三角形,其中∠EBF=90°,
∴BE=BF,
∴∠ABC-∠CBF=∠EBF-∠CBF,
∴∠ABF=∠CBE.
在△ABF和△CBE中,有$\left\{\begin{array}{l}{AB=CB}\\{∠ABF=∠CBE}\\{BF=BE}\end{array}\right.$,
∴△ABF≌△CBE(SAS).
(2)解:△CEF是直角三角形.理由如下:
∵△EBF是等腰直角三角形,
∴∠BFE=∠FEB=45°,
∴∠AFB=180°-∠BFE=135°,
又∵△ABF≌△CBE,
∴∠CEB=∠AFB=135°,
∴∠CEF=∠CEB-∠FEB=135°-45°=90°,
∴△CEF是直角三角形.
点评 本题考查了正方形的性质.全等三角形的判定及性质、等腰直角三角形的性质以及角的计算,解题的关键是:(1)根据判定定理SAS证明△ABF≌△CBE;(2)通过角的计算得出∠CEF=90°.本题属于中档题,难度不大,解决该题型题目时,通过正方形和等腰三角形的性质找出相等的边,再通过角的计算找出相等的角,以此来证明两三角形全等是关键.

练习册系列答案
相关题目
10.平面直角坐标系内的点A(-1,2)与点B(-1,-2)关于( )
| A. | y轴对称 | B. | x轴对称 | C. | 原点对称 | D. | 直线y=x对称 |
14.小颖同学在手工制作中,把一个边长为12cm的等边三角形纸片贴到一个圆形的纸片上,若三角形的三个顶点恰好都在这个圆上,则圆的半径为( )
| A. | 2$\sqrt{3}$cm | B. | 4$\sqrt{3}$cm | C. | 6$\sqrt{3}$cm | D. | 8$\sqrt{3}$cm |
4. 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )
 如图,几何体的俯视图是( )
如图,几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
19.如果方程2xm-1-3y2m+n=1是关于x、y的二元一次方程,那么m、n的值分别为( )
| A. | 1,0 | B. | 2,-3 | C. | 1,-3 | D. | 1,1 |
 如图,P、Q是Rt△ABC斜边AB上的点,AQ=AC,BP=CB,△ABC内切圆半径为5,则△CPQ外接圆半径为5$\sqrt{2}$.
如图,P、Q是Rt△ABC斜边AB上的点,AQ=AC,BP=CB,△ABC内切圆半径为5,则△CPQ外接圆半径为5$\sqrt{2}$.