题目内容
1. 如图,P、Q是Rt△ABC斜边AB上的点,AQ=AC,BP=CB,△ABC内切圆半径为5,则△CPQ外接圆半径为5$\sqrt{2}$.
如图,P、Q是Rt△ABC斜边AB上的点,AQ=AC,BP=CB,△ABC内切圆半径为5,则△CPQ外接圆半径为5$\sqrt{2}$.
分析 如图设⊙O是△ABC内切圆,E、F是切点,连接OE、OF、0A、OB、OC,只要证明点O是△CPQ的外接圆的圆心即可解决问题.
解答 解:如图设⊙O是△ABC内切圆,E、F是切点,连接OE、OF、0A、OB、OC.
∵点O是△ABC内心,
∴OA平分∠CAB,OB平分∠CBA,
∵AC=AQ,BC=BP,
∴AO垂直平分CQ,BO垂直平分PC,
∴点O是△PCQ的外心,
∵∠ECF=∠OEC=∠OFC=90°,
∴四边形OECF是矩形,
∵OE=OF=5,
∴四边形OECF是正方形,
∴OC=$\sqrt{2}$OE=5$\sqrt{2}$,
∴△PCQ的外接圆的半径为5$\sqrt{2}$.
故答案为5$\sqrt{2}$.
点评 本题考查是矩形外接圆、内切圆的性质,内心以及外心的定义等知识,解题的关键是熟练掌握内心、外心的性质,属于填空题中的压轴题.

练习册系列答案
相关题目
2.已知压强的计算公式是P=$\frac{F}{S}$,我们知道,刀具在使用一段时间后,就好变钝,如果刀刃磨薄,刀具就会变得锋利.下列说法中,能正确解释刀具变得锋利这一现象的是( )
| A. | 当受力面积一定时,压强随压力的增大而增大 | |
| B. | 当受力面积一定时,压强随压力的增大而减小 | |
| C. | 当压力一定时,压强随受力面积的减小而减小 | |
| D. | 当压力一定时,压强随受力面积的减小而增大 |
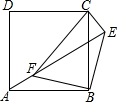 如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.
如图,点E正方形ABCD外一点,点F是线段AE上一点,△EBF是等腰直角三角形,其中∠EBF=90°,连接CE、CF.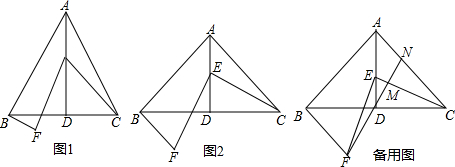
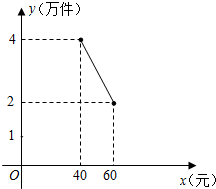 为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.
为了扶持大学生自主创业,市政府提供了80万元无息贷款,用于某大学生开办公司生产并销售自主研发的一种电子产品,并约定用该公司经营的利润逐步偿还无息贷款.已知该产品的生产成本为每件40元,员工每人每月的工资为4000元,公司每月需支付其它费用15万元.该产品每月销售量y(万件)与销售单价x(元)之间的函数关系如图所示.