题目内容
 如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是
如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是考点:旋转的性质
专题:
分析:如图,作辅助线;证明△ABE≌△ADM(SAS),得到∠BAE=∠DAM,AE=AM;证明∠EAF=∠MAF=45°;进而证明△EAF≌△MAF,得到MF=EF,即可解决问题.
解答: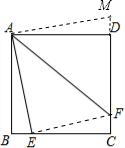 解:如图,延长CD到M,使DM=BE,
解:如图,延长CD到M,使DM=BE,
连接AM、EF;
∵四边形ABCD为正方形,
∴∠B=∠ADC=90°,AB=AD;
在△ABE与△ADM中,
,
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM,AE=AM;
∴∠BAE+DAF=∠DAM+∠DAF=∠MAF;
∵∠EAF=45°,
∴∠BAE+DAF=90°-45°=45°,
∴∠EAF=∠MAF=45°;
在△EAF与△MAF中,
,
∴△EAF≌△MAF(SAS),
∴MF=EF,而MF=MD+DF=BE+DF,
∴BE+DF=EF,
故答案为BE+DF=EF.
 解:如图,延长CD到M,使DM=BE,
解:如图,延长CD到M,使DM=BE,连接AM、EF;
∵四边形ABCD为正方形,
∴∠B=∠ADC=90°,AB=AD;
在△ABE与△ADM中,
|
∴△ABE≌△ADM(SAS),
∴∠BAE=∠DAM,AE=AM;
∴∠BAE+DAF=∠DAM+∠DAF=∠MAF;
∵∠EAF=45°,
∴∠BAE+DAF=90°-45°=45°,
∴∠EAF=∠MAF=45°;
在△EAF与△MAF中,
|
∴△EAF≌△MAF(SAS),
∴MF=EF,而MF=MD+DF=BE+DF,
∴BE+DF=EF,
故答案为BE+DF=EF.
点评:该题以正方形为载体,主要考查了旋转变换的性质、全等三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,构造全等三角形.

练习册系列答案
相关题目
 函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )
函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )| A、a>0 | B、c>0 |
| C、b>0 | D、a+b-c>0 |
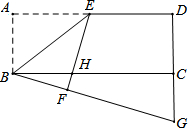 已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH=
已知如图,在矩形ABCD中,点E是AD的中点,连结BE,将△ABE沿着BE翻折得到△FBE,EF交BC于点H,延长BF、DC相交于点G,若DG=16,BC=24,则FH= 如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-
如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-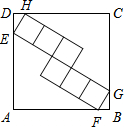 如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为
如图,正方形ABCD的边长为5,内部有6个大小相同的小正方形,小正方形的顶点E、F、G、H分别落在边AD、AB、BC、CD上,则小正方形的边长为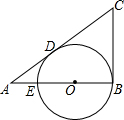 已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )
已知,如图,在△ABC中,∠ABC=90°,在AB上取一点E,以BE为直径的⊙O恰与AC相切于点D.若AE=2cm,AD=4cm,则△ABC的面积为( )