题目内容
 函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )
函数y=ax2+bx+c的图象的右侧如图所示,下列选项不正确的是( )| A、a>0 | B、c>0 |
| C、b>0 | D、a+b-c>0 |
考点:二次函数图象与系数的关系
专题:
分析:首先根据抛物线的图象确定开口方向进而确定a的符号,再依据对称轴的正负和a的符号即可判断b的符号,然后根据与y轴的交点的纵坐标即可判断c的正负,可得a+b-c>0.
解答:解:由图象得开口向上可得a>0,故A正确;
由x=-
<0,可得b>0,故C正确;
由二次函数y=ax2+bx+c的图象交y轴于负半轴可得c<0,故B错误;
∴a+b-c>0,可得D正确.
故选B.
由x=-
| b |
| 2a |
由二次函数y=ax2+bx+c的图象交y轴于负半轴可得c<0,故B错误;
∴a+b-c>0,可得D正确.
故选B.
点评:本题主要考查了二次函数的图象与系数的关系,能根据图象正确确定各个系数的符号是解决此题的关键,此题运用了数形结合思想.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下列说法正确的是( )
| A、直线比射线长 |
| B、过两点有且只有一条直线 |
| C、过三点一定能作出一条直线 |
| D、一个角一定比它的补角小 |
下列等式的变形正确的是( )
A、如果s=vt,那么v=
| ||
B、如果
| ||
| C、如果-x-1=y-1,那么x=y | ||
| D、如果a=b,那么a+2=2+b |
 如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是
如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是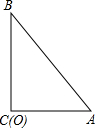 如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.
如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.