题目内容
从2开始的连续偶数相加,它们和的情况如下表:
(1)请猜想:2+4+6+…+200= ;
(2)请猜想:2+4+6+…+2n ;
(3)计算:40+42+44+…+402.
| 加数的个数(n) | 和(S) |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
| … | … |
(2)请猜想:2+4+6+…+2n
(3)计算:40+42+44+…+402.
考点:规律型:数字的变化类
专题:
分析:(1)(2)首先确定有几个加数,由上述可得规律:加数的个数为最后一个加数÷2,据此解答;
(3)把40+42+44+…+402变形为2+4+6+8+…+402-(2+4+6+8+…+38),再进一步利用(2)规律计算即可.
(3)把40+42+44+…+402变形为2+4+6+8+…+402-(2+4+6+8+…+38),再进一步利用(2)规律计算即可.
解答:解:(1)2+4+6+…+200
=100×(100+1)
=10100;
(2)2+4+6+…+2n=n(n+1);
(3)40+42+44+…+402
=2+4+6+8+…+402-(2+4+6+8+…+38)
=201×202-19×20
=40602-380
=40222.
=100×(100+1)
=10100;
(2)2+4+6+…+2n=n(n+1);
(3)40+42+44+…+402
=2+4+6+8+…+402-(2+4+6+8+…+38)
=201×202-19×20
=40602-380
=40222.
点评:此题考查数字的变化规律,学生通过观察,分析、归纳发现其中的规律,并应用发现的规律解决问题.

练习册系列答案
相关题目
在-3、2、0、-1这四个数中,最小的数是( )
| A、-3 | B、-1 | C、0 | D、2 |
 如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )
如图,⊙O与射线AM相切于点B,圆心O在射线AN上,⊙O半径为6cm,OA=10cm.点P从点A出发,以2cm/秒的速度沿AN方向运动,过P点作直线l垂直AB,当l与⊙O相切时,所用时间是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
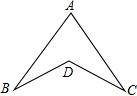 如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于
如图,若AB=AC,BD=CD,∠B=20°,∠BDC=120°,则∠A等于 河上有一座抛物线拱形桥,已知桥下的水面离桥孔顶部3m时,水面宽为6m.当水位上升1m时,水面宽为多少?
河上有一座抛物线拱形桥,已知桥下的水面离桥孔顶部3m时,水面宽为6m.当水位上升1m时,水面宽为多少? 如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是
如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是 如图,△AOB绕点O旋转得到△COD,在这个旋转过程中:
如图,△AOB绕点O旋转得到△COD,在这个旋转过程中: