题目内容
 如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-
如图,一名男生推铅球,铅球进行高度y(m)与水平距离x(m)之间的关系式为:y=-| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
(1)求铅球被推出的最大高度;
(2)若铅球成绩达到11m即为优秀(铅球被推出的水平距离),请通过计算说明该名同学的成绩是否优秀.
考点:二次函数的应用
专题:
分析:(1)将二次函数配方成顶点式后确定铅球的最大高度即可;
(2)成绩就是当高度y=0时x的值,所以解方程可求解.
(2)成绩就是当高度y=0时x的值,所以解方程可求解.
解答:解:(1)∵y=-
x2+
x+
=-
(x-4)2+3,
∴当x=4时,y=3,
即铅球被推出的最大高度为3m;
(2)∵当y=0时,-
x2+
x+
=0,
解得x1=10,x2=-2(不合题意,舍去),
∴推铅球的距离是10米,
∴该同学的成绩没有达到优秀.
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
| 1 |
| 12 |
∴当x=4时,y=3,
即铅球被推出的最大高度为3m;
(2)∵当y=0时,-
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |
解得x1=10,x2=-2(不合题意,舍去),
∴推铅球的距离是10米,
∴该同学的成绩没有达到优秀.
点评:此题考查了二次函数的应用,把函数问题转化为方程问题来解,渗透了函数与方程相结合的解题思想方法.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
下列计算中,正确的是( )
| A、(-1)2×(-1)5=1 | ||||
B、-3÷(-
| ||||
C、
| ||||
| D、-(-3)2=9 |
发射一枚炮弹,经x秒后的高度为y公尺,且时间与高度关系为y=ax2+bx,若此炮弹在第10秒与第20秒时的高度相等,则下列四个时间中,哪一个时间炮弹的高度是最高的?( )
| A、第9秒 | B、第13秒 |
| C、第15秒 | D、第18秒 |
有一列数,前五个数依次为
、-
、
、-
、
,…,则这列数的第n个是( )
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
| 5 |
| 6 |
A、
| ||
B、-
| ||
C、(-1)n
| ||
D、(-1)n+1
|
在-3、2、0、-1这四个数中,最小的数是( )
| A、-3 | B、-1 | C、0 | D、2 |
 河上有一座抛物线拱形桥,已知桥下的水面离桥孔顶部3m时,水面宽为6m.当水位上升1m时,水面宽为多少?
河上有一座抛物线拱形桥,已知桥下的水面离桥孔顶部3m时,水面宽为6m.当水位上升1m时,水面宽为多少? 如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是
如图,自正方形ABCD的顶点A引两条射线分别交BC、CD于E、F,∠EAF=45°,在保持∠EAF=45°的前提下,当点E、F分别在边BC、CD上移动时,BE+DF与EF的关系是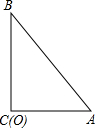 如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.
如图,在Rt△ABC中,∠C=90°,AC=10,BC=24,⊙O的半径为6,当圆心O与C重合时,试判断⊙O与AB的位置关系.