题目内容
7.如图1,已知Rt△ABC,∠BAC=90°,AB=AC,点D是BC的中点.作正方形DEFG,使点A、C分别在DG和DE上,连接AE,BG.(1)试猜想线段BG和AE的数量关系是BG=AE;
(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°),
①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;
②在旋转过程中,当AE取最大值时,请直接写出AF、AE、EF之间的数量关系(写出等式即可).

分析 (1)利用全等三角形△BDG≌△ADE,证明BG=AE;
(2)①与(1)同理,证明△BDG≌△ADE,可得BG=AE,结论依然成立;
②在旋转过程中,当AE取最大值时,点A、D、E共线,△AEF构成直角三角形,因此AF、AE、EF之间的数量关系满足勾股定理.
解答 解:(1)猜想:BG=AE.
证明:在△BDG和△ADE中,
$\left\{\begin{array}{l}BD=AD\\∠BDG=∠ADE=90°\\ DG=ED\end{array}\right.$
∴△BDG≌△ADE(SAS)
∴BG=AE.
(2)①成立.
证明:如答图1,连接AD.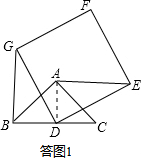
在Rt△ABC中,AB=AC,D为斜边BC的中点,
∴AD=BD,AD⊥BC,
∴∠ADG+∠GDB=90°.
∵四边形EFGD为正方形,
∴DE=DG,且∠GDE=90°,
∴∠ADG+∠ADE=90°,
∴∠BDG=∠ADE.
在△BDG和△ADE中,
$\left\{\begin{array}{l}BD=AD\\∠BDG=∠ADE=90°\\ DG=ED\end{array}\right.$
∴△BDG≌△ADE(SAS)
∴BG=AE.
②AF2=AE2+EF2.理由如下:
在△ADE中,∵AE<AD+DE,
∴当点A、D、E共线时,AE取得最大值,最大值为AD+DE.
作出图形如下: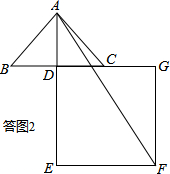
此时△AEF是直角三角形,∴AF2=AE2+EF2.
点评 本题是几何综合题,考查了全等三角形、正方形、等腰直角三角形、旋转、勾股定理等知识点,解题关键是理解(2)②问中“在旋转过程中,当AE取最大值时”的含义.

练习册系列答案
相关题目
15.方程$\frac{2}{x-2}=\frac{1}{x}$的解是( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
2.某商品每件的标价是440元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为( )
| A. | 240元 | B. | 280元 | C. | 320元 | D. | 360元 |
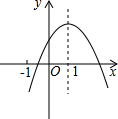 二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( ) 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )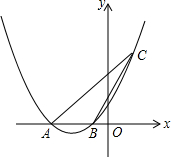 如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧.
如图,二次函数y=$\frac{1}{4}$x2+($\frac{m}{4}$+1)x+m(其中m<4)的图象与x轴相交于A、B两点,且点A在点B的左侧. 某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的俯视图是( )
某运动器材的形状如图所示,以箭头所指的方向为左视方向,则它的俯视图是( )


