题目内容
3. 如图,一山坡的坡比为1:2,某人从山脚下的A点走了500米后到达山顶的点B.那么这人垂直高度上升了100$\sqrt{5}$米.
如图,一山坡的坡比为1:2,某人从山脚下的A点走了500米后到达山顶的点B.那么这人垂直高度上升了100$\sqrt{5}$米.
分析 设这人垂直高度上升x米,根据坡比为1:2,可得此人水平向右走了2x米,然后根据此人沿山坡走了500米,利用勾股定理求解.
解答 解:设这人垂直高度上升x米,则此人水平向右走了2x米,
∵AB=500m,
∴$\sqrt{{x}^{2}+(2x)^{2}}$=500,
解得:x=100$\sqrt{5}$.
故这人垂直高度上升100$\sqrt{5}$米.
故答案为:100$\sqrt{5}$.
点评 本题考查了解直角三角形的应用,解答本题的关键是根据坡比构造直角三角形,利用勾股定理求解,难度一般.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
14. 如图,直线a∥b,∠1=60°,那么∠2的度数是( )
如图,直线a∥b,∠1=60°,那么∠2的度数是( )
 如图,直线a∥b,∠1=60°,那么∠2的度数是( )
如图,直线a∥b,∠1=60°,那么∠2的度数是( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
15.方程$\frac{2}{x-2}=\frac{1}{x}$的解是( )
| A. | 2 | B. | 1 | C. | -2 | D. | -1 |
12. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=-$\frac{1}{3}$,有下列结论:①ab>0;②a+b+c<0;③b+2c<0;其中正确结论的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
13. 如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
 如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )
如图,数轴上两点A,B表示的实数分别为-4和6,这两点的距离是( )| A. | 4 | B. | 6 | C. | 10 | D. | -10 |
 如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,中间将修建一座边长为(a+b)米的正方形雕像,规划部门计划将余下部分进行绿化.
如图,某市有一块长为(3a+b)米、宽为(2a+b)米的长方形地,中间将修建一座边长为(a+b)米的正方形雕像,规划部门计划将余下部分进行绿化.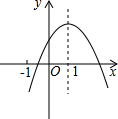 二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( )
二次函数y=ax2+bx+c的图象如图所示,则在下列各不等式中成立的个数是( ) 已知二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是②③④⑥(写出所有正确结论的序号)
已知二次函数y=ax2+bx+c的图象如图所示,对称轴x=1,下列结论中正确的是②③④⑥(写出所有正确结论的序号)