题目内容
11.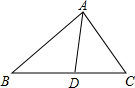 如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,S△ABD=12,则 S△ACD=9cm2.
如图,在△ABC中,AD是它的角平分线,AB=8cm,AC=6cm,S△ABD=12,则 S△ACD=9cm2.
分析 过D作DE⊥AB,DF⊥AC,垂足分别为E、F,由△ABD的面积可求得DE,由角平分线的性质可求得DF,则可求得△ACD的面积.
解答  解:
解:
过D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵AD是角平分线,
∴DE=DF,
∵S△ABD=$\frac{1}{2}$AB•DE,
∴12=$\frac{1}{2}$×8DE,解得DE=3(cm),
∴DF=3cm,
∴S△ACD=$\frac{1}{2}$AC•DF=$\frac{1}{2}$×6×3=9(cm2),
故答案为:9cm2.
点评 本题主要考查角平分线的性质,掌握角平分线上的点到角两边的距离相等是解题的关键.

练习册系列答案
相关题目
2. 如图中∠BOD的度数是( )
如图中∠BOD的度数是( )
 如图中∠BOD的度数是( )
如图中∠BOD的度数是( )| A. | 150° | B. | 125° | C. | 110° | D. | 55° |
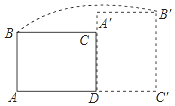 如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).
如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π).