题目内容
3．
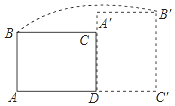如图，在矩形ABCD中，AB=3，AD=4，将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′，则点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是多少？（结果保留π）．
分析 根据点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是=S扇形BDB′+S矩形ABCD求解即可．
解答 解：如图，连接BD与B′D，
点B经过的路径与BA，AC′，C′B′所围成封闭图形的面积是：
S扇形BDB′+S矩形ABCD=$\frac{1}{4}$π×52+3×4=$\frac{25π}{4}$+12．
点评 本题主要考查了扇形的面积计算及旋转的性质，解题的关键是理解点B经过的路径与BA，AC′，C′B′所围成的封闭图形．
练习册系列答案
相关题目
在我国古代数学著作《九章算术》中记载了一道有趣的数学问题：“今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何？”这个数学问题的意思是说：“有一个水池，水面是一个边长为1丈（1丈=10尺）的正方形，在水池正中央长有一根芦苇，芦苇露出水面 1 尺．如果把这根芦苇拉向岸边，它的顶端恰好到达岸边的水面．请问这个水池的深度和这根芦苇的长度各是多少？”设这个水池的深度是x尺，根据题意，可列方程为x2+52=（x+1）2．
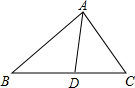如图，在△ABC中，AD是它的角平分线，AB=8cm，AC=6cm，S△ABD=12，则 S△ACD=9cm2．
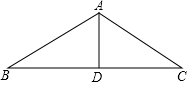已知：如图，△ABC中，D是BC上一点，连接AD，在△ABC的内部是否存在到∠C的两边距离相等的点，在△内部是否存在一点E，改为点到∠B的两边距离相等，又到∠DAC的两边距离相等？（要求写出作法，并保留作图痕迹）
A是双曲线y=-$\frac{5}{x}$上一点，过点A向x轴作垂线，垂足为B，向y轴作垂线，垂足为C，则四边形OBAC的面积为（ ）