题目内容
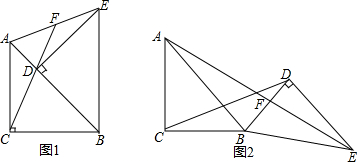
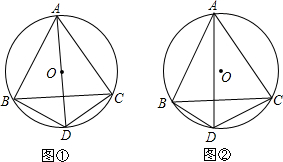
7.已知.Rt△ABC≌Rt△EBD,CD交AE于F.(1)如图1,当Rt△ABC和Rt△EBD均为等腰直角三角形时,若点D落在边AB上,猜想线段AF与线段EF的数量关系,并证明;
(2)如图2,线段AF、EF的数量关系保持不变吗?如果不变,请证明,如果发生改变,请说明理由.
分析 (1)根据全等三角形的性质得到BC=BD,AB=BE,∠ABC=∠ABE=45°,根据等腰三角形的性质得到∠BAE=∠BCD=∠BDC=$\frac{180°-45°}{2}$,等量代换得到∠FAD=∠ADF,由等腰三角形的判定得到AF=DF,根据直角三角形的性质即可得到结论.
(2)连接BF,根据全等三角形的性质得到AB=BE,CB=BD,∠CBA=∠DBE,根据角的和差得到∠CBD=∠ABE,由等腰三角形的性质得到∠CDB=$\frac{180°-∠CBD}{2}$,∠BEA=$\frac{180°-∠ABE}{2}$,推出B,E,D,F四点共圆,根据圆周角定理得到∠BFE=∠BDE=90°,然后根据等腰三角形的性质即可得到结论.
解答 解:(1)AF=EF,
理由:∵Rt△ABC≌Rt△EBD,
∴BC=BD,AB=BE,∠ABC=∠ABE=45°,
∴∠BAE=∠BCD=∠BDC=$\frac{180°-45°}{2}$,
∵∠ADF=∠BDC,
∴∠FAD=∠ADF,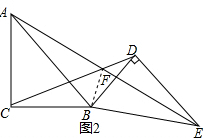
∴AF=DF,
∵∠ADE=90°,
∴∠FDE=∠FED,
∴EF=DF,
∴AF=EF;
(2)连接BF,
∵Rt△ABC≌Rt△EBD,
∴AB=BE,CB=BD,∠CBA=∠DBE,
∴∠CBD=∠ABE,
∴∠CDB=$\frac{180°-∠CBD}{2}$,∠BEA=$\frac{180°-∠ABE}{2}$,
∴∠CDB=∠BEA,
∴B,E,D,F四点共圆,
∴∠BFE=∠BDE=90°,
∴BF⊥AE,
∴AF=EF.
点评 本题考查了全等三角形的性质,等腰直角三角形的性质,四点共圆,圆周角定理,等腰三角形的判定和性质,熟练则各定理是解题的关键.

练习册系列答案
相关题目
18.下列运算正确的是( )
| A. | ${(\frac{2}{3})^2}=\frac{9}{2}$ | B. | ${(-\frac{3}{2})^3}=-\frac{27}{2}$ | C. | ${(-\frac{3}{2})^2}=-\frac{9}{4}$ | D. | ${(-\frac{3}{2})^3}=-\frac{27}{8}$ |
2.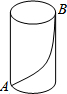 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
 如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )
如图,一只蚂蚁从点A沿圆柱表面爬到点B,如果圆柱的高为8cm,圆柱的底面半径为$\frac{6}{π}$cm,那么最短的路线长是( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 10πcm |
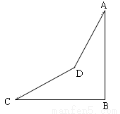
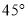 ,沿着坡角为
,沿着坡角为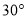 的斜坡前进400米到D处(即
的斜坡前进400米到D处(即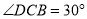 ,
, 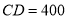 米),测得山顶A的仰角为
米),测得山顶A的仰角为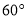 ,求山的高度AB.
,求山的高度AB.