题目内容
2．
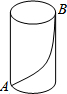如图，一只蚂蚁从点A沿圆柱表面爬到点B，如果圆柱的高为8cm，圆柱的底面半径为$\frac{6}{π}$cm，那么最短的路线长是（ ）| A． | 6cm | B． | 8cm | C． | 10cm | D． | 10πcm |
分析 首先画出示意图，连接AB，根据圆的周长公式算出底面圆的周长，AC=$\frac{1}{2}$×底面圆的周长，再在Rt△ACB中利用勾股定理算出AB的长即可．
解答 解：连接AB，
∵圆柱的底面半径为$\frac{6}{π}$cm，
∴AC=$\frac{1}{2}$×2•π•$\frac{6}{π}$=6（cm），
在Rt△ACB中，AB2=AC2+CB2=36+64=100，
AB=10cm．
故选：C．
点评 此题主要考查了平面展开图，最短路径问题，做此类题目先根据题意把立体图形展开成平面图形后，再确定两点之间的最短路径．一般情况是两点之间，线段最短．在平面图形上构造直角三角形解决问题．
练习册系列答案
名校课堂系列答案
相关题目
17．已知点A（$\sqrt{2}$，y1），B（4，y2），C（-3$\sqrt{5}$，y3）在抛物线y=a（x-2）2+k+2（a＞0）上，则y1、y2、y3的大小关系是（ ）
| A． | y1＞y2＞y3 | B． | y1＞y3＞y2 | C． | y3＞y1＞y2 | D． | y1＜y2＜y3 |
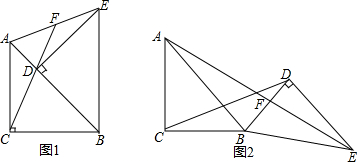
如图，已知∠ACB=90°，AC=BC，BE⊥CE于E，AD⊥CE于D，DE=1.7cm，BE=0.8cm，求线段AD的长．
、
、
、
、
、
、
、
中，分式有（ ）.