题目内容
12.在⊙O中,弦AB=BC=CA,D为$\widehat{BC}$上一点.(不与点B,C重合),连接AD,BD,CD(1)如图①,若点D是$\widehat{BC}$的中点.结论:AD=BD+CD 是否成立?写出判断不用证明;
(2)如图②,若点D在$\widehat{BC}$上移动,结论:AD=BD+CD是否成立?写出判断给出证明;
(3)若BC=3,在(2)的条件下,求BD+CD的取值范围(直接写出结果即可)
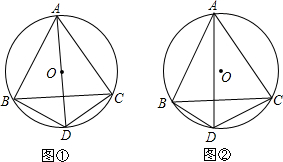
分析 (1)设圆O的半径为R,连接BO、CO,由AB=BC=CA,所以△ABC为等边三角形,再证明△BOD与△COD为等边三角形,所以BD=DC=R,由AD=2R,所以BD+DC=AD.
(2)如图2,延长BD至E点使得CD=DE,证明△ACD≌△BCE(SAS),即可得到AD=BE=BD+DE.
(3)在(2)的条件下,3<BD+DE≤2$\sqrt{3}$.
解答 解:(1)设圆O的半径为R,连接BO、CO,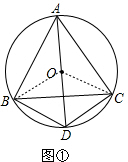
∵AB=BC=CA,
∴△ABC为等边三角形,
∴∠BAC=60°,
∵点D是$\widehat{BC}$的中点,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC=30°,
∴∠BOD=∠COD=60°,
∵OB=OD=OC,
∴△BOD与△COD为等边三角形,
∴BD=DC=R,
∵AD=2R,
∴BD+DC=AD.
(2)如图2,延长BD至E点使得CD=DE,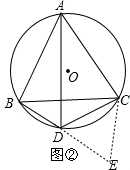
由图2可知∠BDC=120°,
∴∠CDE=60°,△CDE为等边三角形,
∴CD=CE=DE;
∵∠CDE=∠ACB=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,
即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=AB}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS),
∴AD=BE=BD+DE.
(3)在(2)的条件下,
由圆周角定理可得:∠DBC=∠DAC=30°,∠BCD=∠BAD=30°,
∴∠BCE=∠DCE+∠BCD=90°,
∴BE=2CE,
在Rt△BCE中,BC2+CE2=BE2
32+CE2=(2CE)2
解得:CE=$\sqrt{3}$,
则BE=2$\sqrt{3}$,
∴BC+CD=BD+DE=BE=2$\sqrt{3}$,
由三角形两边之和大于第三边,
∴BD+DE>3,
∴3<BD+DE≤2$\sqrt{3}$.
点评 本题考查了全等三角形的性质与判定定理,解决本题的关键是证明三角形全等.

 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
| A. | y=4x2+3 | B. | y=4x2-3 | C. | y=4(x-3)2 | D. | y=4(x+3)2 |
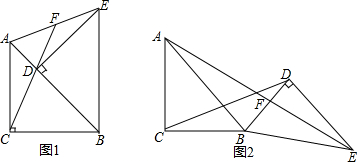
 由8个大小相同的正方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图.
由8个大小相同的正方体搭成的几何体的俯视图如图所示,小正方形中的数字表示在该位置的小正方体的个数,请画出这个几何体的主视图和左视图. 的对称轴为直线
的对称轴为直线 ,与
,与 轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
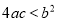 ;② 方程
;② 方程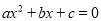 的两个根是
的两个根是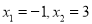 ;③
;③ 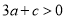 ;④当
;④当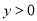 时,
时, 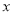 的取值范围是
的取值范围是 ;⑤ 当
;⑤ 当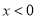 时,
时, 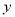 随
随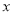 增大而增大;其中结论正确有____.
增大而增大;其中结论正确有____.