题目内容
9. 如图,∠ADE=∠B,∠1=∠2,FG⊥AB,问:CD与AB垂直吗?试说明理由.
如图,∠ADE=∠B,∠1=∠2,FG⊥AB,问:CD与AB垂直吗?试说明理由.
分析 CD与AB垂直,理由为:由同位角相等两直线平行,根据题中角相等得到ED与BC平行,再由两直线平行内错角相等得到∠1=∠BCD,等量代换得到一对同位角相等,利用同位角相等两直线平行得到GF与DC平行,由垂直于平行线中的一条,与另一条也垂直即可得证.
解答 解:CD与AB垂直,理由为:
∵∠ADE=∠B,
∴DE∥BC,
∴∠1=∠BCD,
∵∠1=∠2,
∴∠2=∠BCD,
∴CD∥FG,
∴∠CDB=∠FGB=90°,
∴CD⊥AB.
点评 此题考查了平行线的判定与性质,熟练掌握平行线的性质与判定是解本题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | a3•a2=a6 | B. | (a2)3=a5 | C. | $\sqrt{9}$=3 | D. | 2+$\sqrt{5}$=2$\sqrt{5}$ |
14.用配方法解方程x2-6x+3=0,下列变形正确的是( )
| A. | (x-3)2=6 | B. | (x-3)2=3 | C. | (x-3)2=0 | D. | (x-3)2=1 |
1.在下面四根木棒中,选一根能与长为4cm,9cm的两根木棒首尾依次相接钉成一个三角形的是( )
| A. | 4cm | B. | 5cm | C. | 9cm | D. | 13cm |
 如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.
如图,Rt△ABC中,∠ACB=90°,AC=3cm,BC=6cm,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D,E,则圆O的半径为2cm.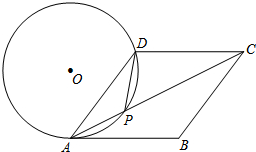 如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.
如图,在菱形ABCD中,P是对角线AC上的一点,且PA=PD,⊙O为△APD的外接圆.