题目内容
13.在Rt△ABC中,∠C=90°,且c=2a,则∠B=60°.分析 首先根据正弦函数的定义求出sinA=$\frac{a}{c}$=$\frac{1}{2}$,利用特殊角的三角函数值得出∠A=30°,再根据直角三角形两锐角互余得出∠B=60°.
解答 解:∵在Rt△ABC中,∠C=90°,且c=2a,
∴sinA=$\frac{a}{c}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠B=90°-∠A=60°.
故答案为60°.
点评 本题考查了直角三角形两锐角互余的性质,正弦函数的定义,特殊角的三角函数值,求出∠A=30°是解题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
4. 如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )
如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )
 如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )
如图,已知A、B、C在⊙O上,∠A=∠B=19°,则∠AOB的度数是( )| A. | 68° | B. | 66° | C. | 78° | D. | 76° |
8.下列运算正确的是( )
| A. | 30=0 | B. | -32=9 | C. | -|-3|=-3 | D. | $\sqrt{9}=±3$ |
 某立体图形的两个视图如图所示,此立体图形可能是圆锥.(写一个即可)
某立体图形的两个视图如图所示,此立体图形可能是圆锥.(写一个即可)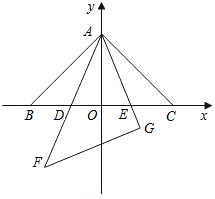 如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论:
如图,在同一平面内,将两个全等的等腰直角三角形ABC和AFG摆放在一起,A为公共顶点,∠BAC=∠AGF=90°,它们的斜边长为2,若△ABC固定不动,△AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n.下列结论: 如图,∠ADE=∠B,∠1=∠2,FG⊥AB,问:CD与AB垂直吗?试说明理由.
如图,∠ADE=∠B,∠1=∠2,FG⊥AB,问:CD与AB垂直吗?试说明理由.