题目内容
12.如图是用棋子摆成的,按照这种摆法,第n个图形中共有n(n+1)枚棋子.
分析 观察每个图形中棋子的个数的规律即可发现有关棋子个数的通项公式,从而得到答案.
解答 解:第一个图形中有1×2=2个棋子,
第二个图形中有2×3=6个棋子,
第三个图形中有3×4=12个棋子,
…
∴第n个图形中共有n(n+1)个棋子,
故答案为:n(n+1).
点评 本题是对图形变化规律的考查,难度中等,发现棋子的规律是解题的关键.

练习册系列答案
相关题目
3.在代数式$\frac{{x}^{2}}{x}$、$\frac{1}{2}$、$\frac{{x}^{2}+1}{2}$、$\frac{3xy}{π}$、$\frac{3}{x+y}$、a+$\frac{1}{m}$中,分式的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.计算(am)3•an的结果是( )
| A. | a${\;}^{{m}^{2}+n}$ | B. | a3m+n | C. | a3(m+n) | D. | a3mn |
1.如图,已知AB∥CD,若按图中规律继续下去,则∠1+∠2+…+∠n=( )
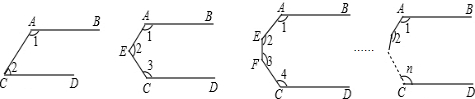

| A. | n•180° | B. | 2n•180° | C. | (n-1)•180° | D. | (n-1)2•180° |
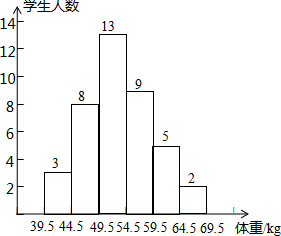 根据某班40名同学的体重频数分布直方图,回答下列问题:
根据某班40名同学的体重频数分布直方图,回答下列问题: