题目内容
已知二次函数y=ax2+bx+c的图象经过点(2,-5),顶点为(-1,4),直线l的解析式为y=2x+m.
(1)求抛物线的解析式;
(2)若抛物线与直线l有两个公共点,求m的取值范围;
(3)若直线l与抛物线只有一个公共点P,求点P的坐标;
(4)设抛物线与x轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
(1)求抛物线的解析式;
(2)若抛物线与直线l有两个公共点,求m的取值范围;
(3)若直线l与抛物线只有一个公共点P,求点P的坐标;
(4)设抛物线与x轴的交点分别为A、B,求在(3)的条件下△PAB的面积.
考点:二次函数综合题
专题:
分析:(1)由抛物线顶点坐标可得二次函数y=a(x+1)2+4,将点(2,-5)代入,即可得到抛物线的解析式,
(2)由抛物线的解析式及直线l的解析式联立,利用△即可求出抛物线与直线l有两个公共点m的取值范围,
(3)由抛物线的解析式及直线l的解析式联立,利用△=0时求出m的值,再联立即可求出点P的坐标,
(4)抛物线的解析式求出AB的长,利用SPAB=
AB•P纵坐标,即可求出△PAB的面积.
(2)由抛物线的解析式及直线l的解析式联立,利用△即可求出抛物线与直线l有两个公共点m的取值范围,
(3)由抛物线的解析式及直线l的解析式联立,利用△=0时求出m的值,再联立即可求出点P的坐标,
(4)抛物线的解析式求出AB的长,利用SPAB=
| 1 |
| 2 |
解答:解:(1)∵抛物线顶点坐标为(-1,4),
∴它的解析式为y=a(x+1)2+4,将点(2,-5)代入,得a=-1.
∴抛物线的解析式为:y=-x2-2x+3.
(2)由
得x2-4x+m-3=0,
∴△=16-4(m-3)=-4m+28.
当-4m+28>0时,解得m<7.
即当m<7时,抛物线与直线l有两个公共点.
(3)由(2)知:当抛物线与直线l只有一个公共点时,m=7,
由
解得
,
即点P的坐标为(-2,3).
(4)∵抛物线的解析式为:y=-x2-2x+3.抛物线与x轴的交点分别为A、B,
∴令0=-x2-2x+3,得x1=-3,x2=1,
∴AB=4,
∴SPAB=
AB•P纵坐标=
×4×3=6.
∴它的解析式为y=a(x+1)2+4,将点(2,-5)代入,得a=-1.
∴抛物线的解析式为:y=-x2-2x+3.
(2)由
|
∴△=16-4(m-3)=-4m+28.
当-4m+28>0时,解得m<7.
即当m<7时,抛物线与直线l有两个公共点.
(3)由(2)知:当抛物线与直线l只有一个公共点时,m=7,
由
|
|
即点P的坐标为(-2,3).
(4)∵抛物线的解析式为:y=-x2-2x+3.抛物线与x轴的交点分别为A、B,
∴令0=-x2-2x+3,得x1=-3,x2=1,
∴AB=4,
∴SPAB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
下列说法正确的是( )
| A、对角线相等且互相垂直的四边形是菱形 |
| B、对角线相等的四边形是矩形 |
| C、若a2=b2,则a=b |
| D、相似三角形对应高的比等于周长的比 |
已知(a+b)2=11,(a-b)2=7,则a2+b2等于( )
| A、4 | B、18 | C、9 | D、8 |
 如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O′,交y轴的负半轴于点C,则点C的坐标为
如图,点A的坐标为(-2,0),点B的坐标为(8,0),以AB为直径作⊙O′,交y轴的负半轴于点C,则点C的坐标为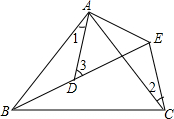 如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=
如图,AB=AC,AD=AE,∠BAC=∠DAE,B、D、E三点在同一条直线上且∠1=25°,∠2=30°,则∠3=