题目内容
5.若等腰三角形的一个内角为40°,则另外两个内角分别是( )| A. | 40°,100° | B. | 70°,70° | ||
| C. | 40°,100°或70°,70° | D. | 以上答案都不对 |
分析 根据等腰三角形的性质,分两种情况讨论:(1)另外两个内角有一个内角是40°;(2)另外两个内角都不是40°;根据三角形的内角和是180°,求出另外两个内角分别是多少度即可.
解答 解:(1)另外两个内角有一个内角是40°时,
另一个内角的度数是:
180°-40°-40°=100°,
∴另外两个内角分别是:40°,100°;
(2)另外两个内角都不是40°时,
另外两个内角的度数相等,都是:
(180°-40°)÷2
=140°÷2
=70°
∴另外两个内角分别是:70°,70°.
综上,可得
另外两个内角分别是:40°,100°或70°,70°.
故选:C.
点评 (1)此题主要考查了等腰三角形的性质和应用,考查了分类讨论思想的应用,要熟练掌握,解答此题的关键是要明确等腰三角形的性质:①等腰三角形的两腰相等;②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(2)此题还考查了三角形的内角和定理的应用,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.方程x(x-3)+x-3=0的解是( )
| A. | 3 | B. | -3,1 | C. | -1 | D. | 3,-1 |
13.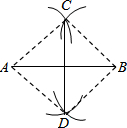 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
 如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )
如图,聪聪在作线段AB的垂直平分线时,他是这样操作的:分别以A和B为圆心,大于$\frac{1}{2}$AB的长为半径画弧,两弧交于C、D,则直线CD即为所求.根据他的作图方法可知四边形ADBC一定是( )| A. | 菱形 | B. | 矩形 | C. | 正方形 | D. | 等腰梯形 |
20.-6的相反数是( )
| A. | 6 | B. | -6 | C. | $\frac{1}{6}$ | D. | $-\frac{1}{6}$ |
10.一个质地均匀的正方体骰子的六个面上分别刻有“我”、“爱”、“爸”、“爸”、“妈”、“妈”六个字,如果将这个骰子掷一次,那么向上一面出现“妈”字的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
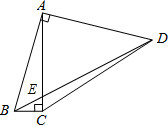 如图,四边形ABCD中,对角线交于点E,∠BAD=∠ACB=90°,AB=AD,若tan∠ABC=4,EC=1,则BE=$\frac{\sqrt{34}}{3}$.
如图,四边形ABCD中,对角线交于点E,∠BAD=∠ACB=90°,AB=AD,若tan∠ABC=4,EC=1,则BE=$\frac{\sqrt{34}}{3}$.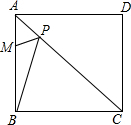 已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.
已知正方形ABCD的一条对角线长为6,M是边AB的一个点,且AM:MB=1:2;P是对角线AC上的一个动点,则PM+PB的最小值=2$\sqrt{5}$.