题目内容
抛物线y=x2-4x+m与x轴的一个交点的坐标为（1，0），则此抛物线与x轴的另一个交点的坐标是____
（3，0）
【解析】把点（1，0）代入抛物线y=x2-4x+m中，得m=3，
所以，原方程为y=x2-4x+3，
令y=0，解方程x2-4x+3=0，得x1=1，x2=3
∴抛物线与x轴的另一个交点的坐标是（3，0）．
故答案为：（3，0）．
在下列图形中，是中心对称图形的是( )
A. 
B. 
C. 
D. 
C
【解析】试题分析：A、旋转180°后不能与自身重合，不是中心对称图形；
B、旋转180°后不能与自身重合，不是中心对称图形；
C、旋转180°后能与自身重合，是中心对称图形；
D、旋转180°后不能与自身重合，不是中心对称图形．
故选C． 观察图象，与图1中的鱼相比，图2中的鱼发生了一些变化．若图1中鱼上点P的坐标为（4，3.2），则这个点在图2中的对应点P1的坐标为__（图中的方格是1×1）．
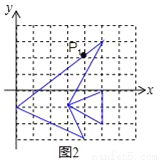
（4，2.2）
【解析】【解析】
由图可知，图1向下平移1个单位，即可得到图2。
∵点P的坐标为（4，3.2），∴点P1的坐标为（4，2.2）．
故答案为：（4，2.2）． 在平面直角坐标系中，点P（-1，2）向右平移3个单位长度得到的点的坐标是 ______ ．
（2，2）．
【解析】试题分析：点P（﹣1，2）向右平移3个单位长度得到的点的坐标是（﹣1+3，2），即（2，2）．故答案为：（2，2）． 已知一元二次方程x2+px+q+1=0的一根为2．
（1）求q关于p的关系式；
（2）求证：抛物线y=x2+px+q与x轴有两个交点；
（1）q= -2p-5；（2）见解析
【解析】试题分析：（1）把x=2代入可求得q与p的关系式；
（2）由△=b2-4ac可判断抛物线与x轴的交点情况.
试题解析：（1）把x=2代入得22+2p+q+1=0，即q= -2p-5；
（2）∵△=p2-4q＞0，
由（1）得△=p2+4（2p+5）=p2+8p+20=（p+4）2+4＞0，
∴一元二次方程x2+px+... 已知抛物线y=x2-x-1与x轴的交点为（m，0），则代数式m2-m+2011的值为（ ）
A. 2009 B. 2012 C. 2011 D. 2010
B
【解析】∵物线y=x2-x-1与x轴的交点为（m，0），
∴将x=m，y=0代入抛物线解析式得：m2-m-1=0，
∴m2-m=1，
则m2-m+2011=1+2011=2012．
故选：B. 抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），这条抛物线的对称轴是（ ）
A. 直线x=1 B. 直线x= -1 C. 直线x=2 D. 直线x= -2
A
【解析】∵抛物线y=ax2+bx+c（a≠0）与x轴的交点是（-2，0）和（4，0），
∴这条抛物线的对称轴是：x=，即x=1；
故选：A． 下列多项式中能用平方差公式分解因式的是（ ）
A．a2+（﹣b）2 B．5m2﹣20mn C．﹣x2﹣y2 D．﹣x2+9
D．
【解析】
试题分析：A、a2+（﹣b）2符号相同，不能用平方差公式分解因式，故A选项错误；
B、5m2﹣20mn两项不都是平方项，不能用平方差公式分解因式，故B选项错误；
C、﹣x2﹣y2符号相同，不能用平方差公式分解因式，故C选项错误；
D、﹣x2+9=﹣x2+32，两项符号相反，能用平方差公式分解因式，故D选项正确．
故选D． 气象台发布的卫星云图显示,代号为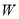
的台风在某海岛(设为点
)的南偏东
方向的
点生成,测得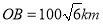
.台风中心从点
以
的速度向正北方向移动，经
后到达海面上的点
处.因受气旋影响,台风中心从点
开始以
的速度向北偏西
方向继续移动.以
为原点建立如图所示的直角坐标系．
(1)台风中心生成点
的坐标为 ,台风中心转折点
的坐标为 ；(结果保留根号)
(2)已知距台风中心
范围内均会受到台风侵袭.如果某城市(设为点
)位于点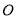
的正北方向且处于台风中心的移动路线上,那么台风从生成到最初侵袭该城要经过多长时间？
（1）（2）台风从生成到最初侵袭该城要经过小时
【解析】试题分析：(1)、根据直角三角形中特殊角的三角函数值分别求出点B和点C的坐标；(2)、过点C作CD⊥OA于点D，则∠ACD=30°，根据Rt△ACD中∠ACD的余弦值得出AC的长度，从而求出时间得出答案．
试题解析：(1) :
(2)过点作于点,则,
在Rt中, ，
∴，
∵， ，
∴台风从生成到最初...