题目内容
17.在△ABC中,∠ACB=90°,CD⊥AB于D,AD:BD=2:3,则△ACD与△CBD的相似比为$\frac{\sqrt{6}}{3}$.分析 分别根据直角三角形的性质和相似三角形的性质直接解答即可.
解答  解:∵AD:BD=2:3,
解:∵AD:BD=2:3,
∴设AD=2x,BD=3x,则AB=5x.
∵△ABC中,∠ACB=90°,CD⊥AB于点D
∴△BCD∽△BAC
∴$\frac{AB}{BC}$=$\frac{BC}{BD}$,
∴BC2=BD•AB=15x2,
∴在直角△ABC中,由勾股定理得到:AC2=AB2-BC2=10x2.
又∵△ACD∽△CBD,
∴($\frac{AC}{BC}$)2=$\frac{10{x}^{2}}{15{x}^{2}}$=$\frac{2}{3}$,
则该相似三角形的相似比是:$\frac{AC}{BC}$=$\frac{\sqrt{6}}{3}$.
故答案是:$\frac{\sqrt{6}}{3}$.
点评 本题考查的是相似三角形的判定与性质,解此题的关键是要知道直角三角形斜边上的高把这个三角形分得的两个小三角形,与原三角形相似.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9. 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
 中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )
中国航母辽宁舰(如图)是中国人民海军第一艘可以搭载固定翼飞机的航空母舰,满载排水量为67500吨,这个数据用科学记数法表示为( )| A. | 6.75×103吨 | B. | 6.75×104吨 | C. | 6.75×105吨 | D. | 6.75×10-4吨 |
12. 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
 如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )
如图,在△ABC中,已知点D、E分别为边BC、AD、上的中点,且S△ABC=4cm2,则S△BEC的值为( )| A. | 2cm2 | B. | 1cm2 | C. | 0.5cm2 | D. | 0.25cm2 |
9.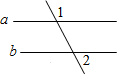 如图,已知∠1=100°,若要使a∥b,则∠2=( )
如图,已知∠1=100°,若要使a∥b,则∠2=( )
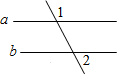 如图,已知∠1=100°,若要使a∥b,则∠2=( )
如图,已知∠1=100°,若要使a∥b,则∠2=( )| A. | 100° | B. | 60° | C. | 40° | D. | 80° |
6.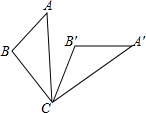 如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
 如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转60°后得到△A′B′C,若∠A=40°,∠B=110°,则∠BCA′的度数是( )| A. | 100° | B. | 90° | C. | 70° | D. | 110° |