题目内容
甲、乙两门大炮在相同的条件下向同一目标个发射50发炮弹,炮弹落点情况如下表所示:
(1)分别计算两门大炮所发射的炮弹落点与目标距离的平均数;
(2)哪门大炮射击的准确性好?
| 炮弹落点与目标距离/km | 40 | 30 | 20 | 10 | 0 |
| 甲发射的炮弹个数 | 0 | 1 | 3 | 7 | 39 |
| 乙发射的炮弹个数 | 1 | 3 | 2 | 3 | 41 |
(2)哪门大炮射击的准确性好?
考点:方差,加权平均数
专题:
分析:(1)根据平均数的计算公式先列出算式,再进行计算即可;
(2)根据方差公式先求出甲、乙的方差,再进行比较,即可得出答案.
(2)根据方差公式先求出甲、乙的方差,再进行比较,即可得出答案.
解答:解:(1)根据题意得:
甲大炮所发射的炮弹落点与目标距离的平均数是:(40×0+30×1+20×3+10×7+0×39)÷50=3.2(m),
乙大炮所发射的炮弹落点与目标距离的平均数是:(40×1+30×3+20×2+10×3+0×41)÷50=4(m),
答:甲、乙两门大炮所发射的炮弹落点与目标距离的平均数分别是3.2m、4m;
(2)根据题意得:
∵S甲2=
[0×(40-3.2)2+1×(30-3.2)2+3×(20-3.2)2+7×(10-3.2)2+39×(0-3.2)2]=45.76,
S乙2=
[(40-4)2+3×(30-4)2+2×(20-4)2+3×(10-4)2+41×(0-4)2]=92,
∴S2甲<S2乙,
∴甲大炮射击的稳定性好.
甲大炮所发射的炮弹落点与目标距离的平均数是:(40×0+30×1+20×3+10×7+0×39)÷50=3.2(m),
乙大炮所发射的炮弹落点与目标距离的平均数是:(40×1+30×3+20×2+10×3+0×41)÷50=4(m),
答:甲、乙两门大炮所发射的炮弹落点与目标距离的平均数分别是3.2m、4m;
(2)根据题意得:
∵S甲2=
| 1 |
| 50 |
S乙2=
| 1 |
| 50 |
∴S2甲<S2乙,
∴甲大炮射击的稳定性好.
点评:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
一种药品现在售价每盒52元,比原来降低了20%,则该药品的原售价是每盒( )
| A、72元 | B、68元 |
| C、65元 | D、56元 |
要使代数式
的值小于2x-7,则x的取值范围是( )
| 6-3x |
| 3 |
| A、x>-3 | ||
| B、x<3 | ||
| C、x>3 | ||
D、x>
|
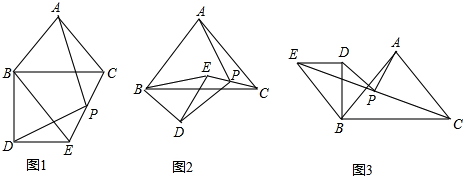
 如图,∠1=∠2=∠3.
如图,∠1=∠2=∠3.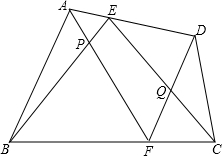 已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.
已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.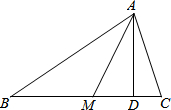 如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.
如图,在△ABC中,∠C=60°,AM是△ABC的角平分线,AD是△ABC的高线.