Question

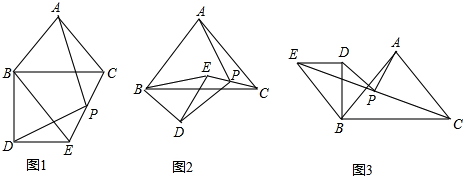
如图1、图2、图3所示，在△ABC和△BDE中，若∠BAC=∠BDE=90°，AB=AC，BD=DE，连CE，点P是CE的中点，则AP与DP有何关系？请分别作出证明．

Answer 1

考点：全等三角形的判定与性质,等腰直角三角形,三角形中位线定理

专题：

分析：M、N是BC、BE的中点，连接AM、PM，DN、PN，根据三角形的中位线定理得出PM=

1

2

BE，PN=

1

2

BC，PM∥DE，PN∥BC，根据两直线平行同位角相等得出∠ENP=∠EBC，∠CMP=∠EBC，进而得出∠ENP=∠CMP，根据等腰直角三角形斜边的中线等于斜边的一半得出AM=

1

2

BC，DN=

1

2

BE，以及AM⊥BC，BN⊥BE，进而求得∠AMP=∠PND，AM=PN，PM=DN，然后根据SAS即可求得△AMP≌△PND，根据全等三角形的对应边相等求得AP=DP．

解答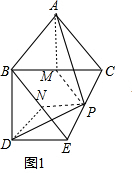：答：AP=DP；．
证明：M、N是BC、BE的中点，连接AM、PM，DN、PN，
如图1，∵PM、PN是三角形的中位线，
∴PM=

1

2

BE，PN=

1

2

BC，PM∥DE，PN∥BC，
∴∠ENP=∠EBC，∠CMP=∠EBC，
∴∠ENP=∠CMP，
∵∠BAC=∠BDE=90°，AB=AC，BD=DE，
∴△ABC与△BDE是等腰直角三角形，
∴AM=

1

2

BC，DN=

1

2

BE，AM⊥BC，BN⊥BE，
∴∠ENP+∠DNE=∠CMP+∠AMC，
∴∠AMP=∠PND，AM=PN，PM=DN，
在△AMP与△PND中

AM=PN ∠AMP=∠PND PM=DN

∴△AMP≌△PND（SAS），
∴AP=DP；
如图2，∵PM、PN是三角形的中位线，
∴PM=

1

2

BE，PN=

1

2

BC，PM∥DE，PN∥BC，
∴∠ENP=∠EBC，∠CMP=∠EBC，
∴∠ENP=∠CMP，
∵∠BAC=∠BDE=90°，AB=AC，BD=DE，
∴△ABC与△BDE是等腰直角三角形，
∴AM=

1

2

BC，DN=

1

2

BE，AM⊥BC，BN⊥BE，
∴∠DNE-∠ENP=∠AMC-∠CMP，
∴∠AMP=∠PND，AM=PN，PM=DN，
在△AMP与△PND中

AM=PN ∠AMP=∠PND PM=DN

∴△AMP≌△PND（SAS），
∴AP=DP；
如图3，∵PM、PN是三角形的中位线，
∴PM=

1

2

BE，PN=

1

2

BC，PM∥DE，PN∥BC，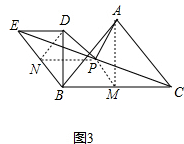
∴∠ENP=∠EBC，∠CMP=∠EBC，
∴∠ENP=∠CMP，
∵∠BAC=∠BDE=90°，AB=AC，BD=DE，
∴△ABC与△BDE是等腰直角三角形，
∴AM=

1

2

BC，DN=

1

2

BE，AM⊥BC，BN⊥BE，
∴∠ENP-∠DNE=∠CMP-∠AMC，
∴∠AMP=∠PND，AM=PN，PM=DN，
在△AMP与△PND中

AM=PN ∠AMP=∠PND PM=DN

∴△AMP≌△PND（SAS），
∴AP=DP．

点评：本题考查了等腰直角三角形的性质，三角形的中位线的性质定理，三角形全等的判定和性质，熟练掌握这些性质和定理是解题的关键．