题目内容
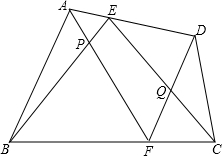 已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.
已知在任意四边形ABCD中,点E、F分别将AD、BC分成两部分,AF和BE交于P,CE和DF交于Q,求证:S四边形EPFQ=S△CDQ+S△ABP.考点:面积及等积变换
专题:证明题
分析:作AG⊥BC于G,EH⊥BC于H,DK⊥BC于K,过D点作DM⊥AG于M,交EH于N,根据三角形面积公式得到S△ABF=
AG•BF,S△DCF=
DK•FC,S△EBC=
EH•BC,
由于DM⊥AM,易得MG=NH=DK,则S△ABF=
AM•BF+
DK•BF,再证明△DNE∽△DMA,利用相似比可得到AM=
EN,由CF:BF=m:n得到BF=
BC,
然后把S△ABF+S△DCF进行变形得到S△ABF+S△DCF=
EH•BC,则S△ABF+S△DCF=S△EBC,最后利用面积的和差即可得到结论.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
由于DM⊥AM,易得MG=NH=DK,则S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| m+n |
| n |
| n |
| m+n |
然后把S△ABF+S△DCF进行变形得到S△ABF+S△DCF=
| 1 |
| 2 |
解答:证明:作AG⊥BC于G,EH⊥BC于H,DK⊥BC于K,过D点作DM⊥AG于M,交EH于N,如图,
点E、F分别将AD、BC分成两部分的比为m:n,即AE:ED=CF:BF=m:n,
S△ABF=
AG•BF,S△DCF=
DK•FC,S△EBC=
EH•BC,
∵DM⊥AM,
∴MG=NH=DK,
∴S△ABF=
(AM+DK)•BF=
AM•BF+
DK•BF,
∵EN∥AM,
∴△DNE∽△DMA,
而AE:ED=m:n,
∴
=
=
,
∴AM=
EN,
∵CF:BF=m:n,
∴BF=
BC,
∴S△ABF+S△DCF=
AM•BF+
DK•BF+
DK•FC=
AM•BF+
DK•BC=
•
EN•
BC+
DK•BC=
EN•BC+
DK+BC=
(EN+DK)•BC=
(EN+NH)•BC=
=
EH•BC,
∴S△ABF+S△DCF=S△EBC,
∴S△ABP+S△PBF+S△CDQ+S△QFC=S四边形EPFQ+S△PBF+S△QFC,
∴S四边形EPFQ=S△CDQ+S△ABP.

点E、F分别将AD、BC分成两部分的比为m:n,即AE:ED=CF:BF=m:n,
S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵DM⊥AM,
∴MG=NH=DK,
∴S△ABF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵EN∥AM,
∴△DNE∽△DMA,
而AE:ED=m:n,
∴
| EN |
| AM |
| DE |
| DA |
| n |
| m+n |
∴AM=
| m+n |
| n |
∵CF:BF=m:n,
∴BF=
| n |
| m+n |
∴S△ABF+S△DCF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| m+n |
| n |
| n |
| m+n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
∴S△ABF+S△DCF=S△EBC,
∴S△ABP+S△PBF+S△CDQ+S△QFC=S四边形EPFQ+S△PBF+S△QFC,
∴S四边形EPFQ=S△CDQ+S△ABP.
点评:本题考查了面积及等积变换:三角形面积等于底与高的积的一半;相似三角形面积的比等于相似比的平方;同底等高的三角形的面积相等.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )
| A、3,4,5 | ||
| B、6,8,10 | ||
C、1,1,
| ||
| D、5,12,13 |
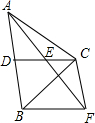 如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF.
如图,在△ABC中,CD是AB边上的中线,E是CD的中点,过点C作AB的平行线交于AE的延长线于F,连接BF.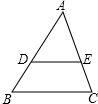 如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=
如图,在△ABC中,DE∥BC,交AB、AC于点D、E,且AD:DB=3:2,若梯形DBCE的面积等于32,则S△ABC=