题目内容
10.把下列各式化成最简二次根式:(1)$\sqrt{150}$;
(2)$\sqrt{\frac{14}{3}}$.
分析 (1)先把被开方数分解质因数,再根据二次根式的性质化成最简即可;
(2)先根据分式除法的逆运算写成两个二次根式的除法,再根据分母有理化计算即可.
解答 解:(1)$\sqrt{150}$=$\sqrt{25×6}$=5$\sqrt{6}$
(2)$\sqrt{\frac{14}{3}}$=$\frac{\sqrt{14}}{\sqrt{3}}$=$\frac{\sqrt{42}}{3}$
点评 本题考查了二次根式的化简及最简二次根式的知识,解题的关键是将被开方数化为能直接开方的因数与另外因数的积的形式和掌握分母有理化的方法.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目
20.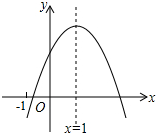 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,下列结论中错误的是( )| A. | abc<0 | B. | 2a+b=0 | C. | b2-4ac>0 | D. | a-b+c>0 |
5.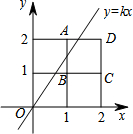 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
 将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )
将2×2的正方形网格如图放置在平面直角坐标系中,每个小正方形的顶点称为格点,每个小正方形的边长都是1,正方形ABCD的顶点都在格点上.若直线y=kx(k≠0)与正方形ABCD有公共点,则k的取值范围是( )| A. | k≤2 | B. | $k≥\frac{1}{2}$ | C. | $\frac{1}{2}≤k≤2$ | D. | $\frac{1}{2}<k<2$ |
12.关于一次函数y=kx-2k图象,下列正确的是( )
| A. |  | B. |  | C. |  | D. |  |
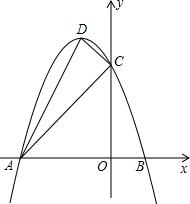 如图,二次函数y=ax2+bx+c(a<0)图象的顶点为D,与x轴的两个交点分别为A、B(A在B左侧),与y轴交于点C(0,3),且OA=3OB,∠ACD=90°
如图,二次函数y=ax2+bx+c(a<0)图象的顶点为D,与x轴的两个交点分别为A、B(A在B左侧),与y轴交于点C(0,3),且OA=3OB,∠ACD=90°