题目内容
3.如图,图(1)或图(2)两个图形都是用四个全等的直角三角形围成的图形,请你选择图(1)或图(2)中的有关面积的等量关系证明数学中的勾股定理.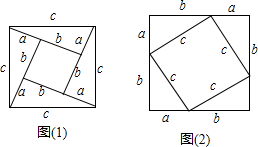
分析 利用四个直角三角形三角形的面积加上中间正方形的面积,得出大正方形的面积,整理得出勾股定理即可.
解答 解:①如图1正方形的面积=c2,
用三角形的面积与边长为a-b的正方形的面积表示为4×$\frac{1}{2}$ab+(b-a)2,
即c2=4×$\frac{1}{2}$ab+(b-a)2化简得a2+b2=c2.
②如图2正方形的面积=(a+b)2,
用三角形的面积与边长为c的正方形的面积表示为4×$\frac{1}{2}$ab+c2,
即(a+b)2=4×$\frac{1}{2}$ab+c2化简得a2+b2=c2.
点评 此题考查勾股定理的证明,利用面积方法建立等式是证明勾股定理常用的方法.

练习册系列答案
相关题目
19.若两个有理数之和大于0,则这两个数一定不是( )
| A. | 两个负数 | B. | 两个正数 | ||
| C. | 一个正数,一个负数 | D. | 一个正数,一个零 |