题目内容
5.已知一次函数y=kx+b的图象过点(1,-1)且不经过第一象限,设m=k2-$\frac{2}{3}$b,则m的取值范围是$\frac{5}{9}$≤m≤1.分析 根据题意得出-1=k+b,k<0,b<0,进而得出m=k2+$\frac{2}{3}$k+$\frac{2}{3}$=(k+$\frac{1}{3}$)2+$\frac{5}{9}$,根据k的取值,即可求得m的取值范围.
解答 解:∵一次函数y=kx+b的图象过点(1,-1)且不经过第一象限,
∴-1=k+b,k<0,b≤0,
∴b=-1-k,
∴-1≤k<0
∵m=k2-$\frac{2}{3}$b,
∴m=k2+$\frac{2}{3}$k+$\frac{2}{3}$=(k+$\frac{1}{3}$)2+$\frac{5}{9}$,
∴k=-$\frac{1}{3}$时,m有最小值为$\frac{5}{9}$,
∵k=-1时,m=1,
∴$\frac{5}{9}$≤m≤1.
点评 本题考查了一次函数的性质,根据性质得出k的取值是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.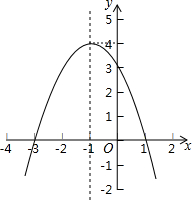 已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:
已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:
(1)求抛物线的表达式;
(2)若该抛物线经过一次平移后过原点O,请写出一种平移方法,并写出平移后得到的新抛物线的表达式.
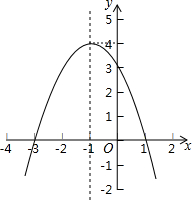 已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:
已知抛物线y=ax2+bx+c如图所示,请结合图象中所给信息完成以下问题:(1)求抛物线的表达式;
(2)若该抛物线经过一次平移后过原点O,请写出一种平移方法,并写出平移后得到的新抛物线的表达式.
 如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动.
如图,射线OM上有三点A、B、C,满足OA=60cm,AB=60cm,BC=10cm(如图所示),点P从点O出发,沿OM方向以1cm/秒的速度匀速运动.