题目内容
13.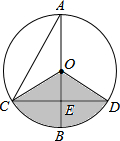 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )| A. | $\frac{2\sqrt{3}π}{9}$ | B. | $\frac{4\sqrt{3}π}{9}$ | C. | $\frac{2π}{9}$ | D. | $\frac{4π}{9}$ |
分析 由AC=2,AE=$\sqrt{3}$,CE=1,根据勾股定理的逆定理可判断△ACE为直角三角形,然后由sinA=$\frac{1}{2}$,可得∠A=30°,然后根据圆周角定理可得:∠COB=60°,然后由∠AEC=90°,可得AE⊥CD,然后根据垂径定理可得:$\widehat{BC}=\widehat{BD}$,进而可得:∠BOD=∠COB=60°,进而可得∠COD=120°,然后在Rt△OCE中,根据sin∠COE=$\frac{CE}{OC}$,计算出OC的值,然后根据扇形的面积公式:S扇形DAB=$\frac{nπ{r}^{2}}{360}$,计算即可.
解答 解:∵AE2+CE2=4=AC2,
∴△ACE为直角三角形,且∠AEC=90°,
∴AE⊥CD,
∴$\widehat{BC}=\widehat{BD}$,
∴∠BOD=∠COB,
∵sinA=$\frac{CE}{AC}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠COB=2∠A=60°,
∴∠BOD=∠COB=60°,
∴∠COD=120°,
在Rt△OCE中,
∵sin∠COE=$\frac{CE}{OC}$,
即sin60°=$\frac{1}{OC}$,
解得:OC=$\frac{2\sqrt{3}}{3}$,
∴S扇形OCD=$\frac{nπ{r}^{2}}{360}$=$\frac{120π×\frac{4}{3}}{360}$=$\frac{4}{9}π$.
故选D.
点评 此题考查了扇形的面积公式,勾股定理的逆定理,圆周角定理及解直角三角形等知识,解题的关键是:据勾股定理的逆定理判断△ACE为直角三角形.

练习册系列答案
相关题目
8.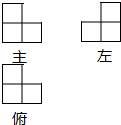 由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
 由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )
由若干个边长为1cm的正方体堆积成一个几何体,它的三视图如图,则这个几何体的表面积是( )| A. | 15cm2 | B. | 18cm2 | C. | 21cm2 | D. | 24cm2 |
18.下列图标既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
5.若用一张直径为20cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )
| A. | 5$\sqrt{3}$cm | B. | 5$\sqrt{5}$cm | C. | $\frac{5\sqrt{15}}{2}$cm | D. | 10cm |
3.“魅力凉都六盘水”某周连续7天的最高气温(单位℃)是26,24,23,18,22,22,25,则这组数据的中位数是( )
| A. | 18 | B. | 22 | C. | 23 | D. | 24 |
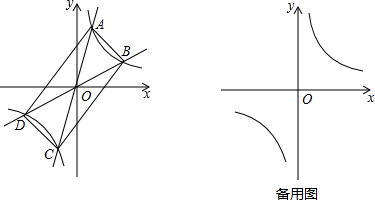
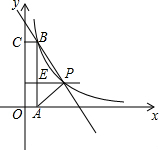 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).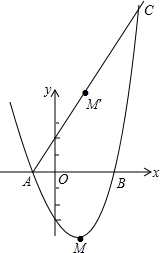 如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.
如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点,顶点M关于x轴的对称点是M′.