题目内容
4.如图,过原点的直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象分别交于两点A,C和B,D,连接AB,BC,CD,DA.(1)四边形ABCD一定是平行四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时k1,k2之间的关系式;若不能,说明理由;
(3)设P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=$\frac{1}{x}$图象上的任意两点,a=$\frac{{y}_{1}+{y}_{2}}{2}$,b=$\frac{2}{{x}_{1}+{x}_{2}}$,试判断a,b的大小关系,并说明理由.
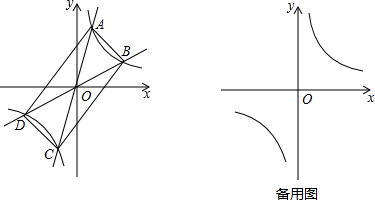
分析 (1)由直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象关于原点对称,即可得到结论.
(2)联立方程求得A、B点的坐标,然后根据OA=OB,依据勾股定理得出 $\sqrt{\frac{1}{{k}_{1}}{+k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}{+k}_{2}}$,两边平分得$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,整理后得(k1-k2)(k1k2-1)=0,根据k1≠k2,则k1k2-1=0,即可求得;
(3)由P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=$\frac{1}{x}$图象上的任意两点,得到y1=$\frac{1}{{x}_{1}}$,y2=$\frac{1}{{x}_{2}}$,求出a=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}}{2}$=$\frac{{x}_{1}{+x}_{2}}{{{2x}_{1}x}_{2}}$,得到a-b=$\frac{{x}_{1}{+x}_{2}}{{{2x}_{1}x}_{2}}$-$\frac{2}{{x}_{1}+{x}_{2}}$=$\frac{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}{{{2x}_{1}x}_{2}{(x}_{1}{+x}_{2})}$=$\frac{{{(x}_{1}{-x}_{2})}^{2}}{{{2x}_{1}x}_{2}{(x}_{1}{+x}_{2})}$>0,即可得到结果.
解答 解:(1)∵直线y=k1x和y=k2x与反比例函数y=$\frac{1}{x}$的图象关于原点对称,
∴OA=OC,OB=OD,
∴四边形ABCD 是平行四边形;
故答案为:平行;
(2)解:∵正比例函数y=k1x(k1>0)与反比例函数y=$\frac{1}{x}$的图象在第一象限相交于A,
∴k1x=$\frac{1}{x}$,解得x=$\sqrt{\frac{1}{{k}_{1}}}$(因为交于第一象限,所以负根舍去,只保留正根)
将x=$\sqrt{\frac{1}{{k}_{1}}}$带入y=k1x得y=$\sqrt{{k}_{1}}$,
故A点的坐标为($\sqrt{\frac{1}{{k}_{1}}}$,$\sqrt{{k}_{1}}$)同理则B点坐标为($\sqrt{\frac{1}{{k}_{2}}}$,$\sqrt{{k}_{2}}$),
又∵OA=OB,
∴$\sqrt{\frac{1}{{k}_{1}}{+k}_{1}}$=$\sqrt{\frac{1}{{k}_{2}}{+k}_{2}}$,两边平方得:$\frac{1}{{k}_{1}}$+k1=$\frac{1}{{k}_{2}}$+k2,
整理后得(k1-k2)(k1k2-1)=0,
∵k1≠k2,
所以k1k2-1=0,即k1k2=1;
(3)∵P(x1,y1),Q(x2,y2)(x2>x1>0)是函数y=$\frac{1}{x}$图象上的任意两点,
∴y1=$\frac{1}{{x}_{1}}$,y2=$\frac{1}{{x}_{2}}$,
∴a=$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{\frac{1}{{x}_{1}}+\frac{1}{{x}_{2}}}{2}$=$\frac{{x}_{1}{+x}_{2}}{{{2x}_{1}x}_{2}}$,
∴a-b=$\frac{{x}_{1}{+x}_{2}}{{{2x}_{1}x}_{2}}$-$\frac{2}{{x}_{1}+{x}_{2}}$=$\frac{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}{{{2x}_{1}x}_{2}{(x}_{1}{+x}_{2})}$=$\frac{{{(x}_{1}{-x}_{2})}^{2}}{{{2x}_{1}x}_{2}{(x}_{1}{+x}_{2})}$,
∵x2>x1>0,
∴${{(x}_{1}{-x}_{2})}^{2}$>0,x1x2>0,(x1+x2)>0,
∴$\frac{{{(x}_{1}{-x}_{2})}^{2}}{{{2x}_{1}x}_{2}{(x}_{1}{+x}_{2})}$>0,
∴a-b>0,
∴a>b.
点评 本题考查了反比例函数的性质,平行四边形的判定,矩形的判定和性质,比较代数式的大小,掌握反比例函数图形上点的坐标的特征是解题的关键.

| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是 (x-60)元;②月销量是 (400-2x)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
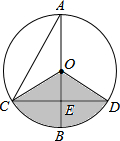 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )| A. | $\frac{2\sqrt{3}π}{9}$ | B. | $\frac{4\sqrt{3}π}{9}$ | C. | $\frac{2π}{9}$ | D. | $\frac{4π}{9}$ |
 课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 150 |
| 不及格 | 50 |
(1)a=200,b=600;
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.
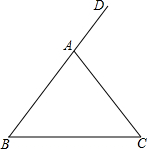 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角. 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点. 如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则k2的值是( )
如图,在平面直角坐标系系中,直线y=k1x+2与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$在第一象限内的图象交于点B,连接BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$,则k2的值是( )