题目内容
5.若用一张直径为20cm的半圆形铁片做一个圆锥的侧面,接缝忽略不计,则所得圆锥的高为( )| A. | 5$\sqrt{3}$cm | B. | 5$\sqrt{5}$cm | C. | $\frac{5\sqrt{15}}{2}$cm | D. | 10cm |
分析 设这个圆锥的底面半径为r,根据圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式得到2πr=$\frac{180•π•10}{180}$,解得r=5,然后利用勾股定理计算这个圆锥的高.
解答 解:设这个圆锥的底面半径为r,
根据题意得2πr=$\frac{180•π•10}{180}$,解得r=5,
所以这个圆锥的高=$\sqrt{1{0}^{2}-{5}^{2}}$=5$\sqrt{3}$(cm).
故选A.
点评 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.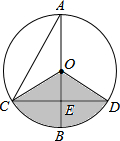 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )| A. | $\frac{2\sqrt{3}π}{9}$ | B. | $\frac{4\sqrt{3}π}{9}$ | C. | $\frac{2π}{9}$ | D. | $\frac{4π}{9}$ |
14. 课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
解答下列问题:
(1)a=200,b=600;
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.
 课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.
课题小组从某市20000名九年级男生中,随机抽取了1000名进行50米跑测试,并根据测试结果绘制了如下尚不完整的统计图表.| 等级 | 人数/名 |
| 优秀 | a |
| 良好 | b |
| 及格 | 150 |
| 不及格 | 50 |
(1)a=200,b=600;
(2)补全条形统计图;
(3)试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.
15.某班组织了一次读书活动,统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这10名同学一周内累计读书时间的中位数是( )
| 一周内累计的读书时间(小时) | 5 | 8 | 10 | 14 |
| 人数(个) | 1 | 4 | 3 | 2 |
| A. | 8 | B. | 7 | C. | 9 | D. | 10 |
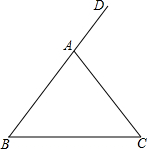 如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
 如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为6π(结果保留π).
如图,PA是⊙O的切线,A是切点,PA=4,OP=5,则⊙O的周长为6π(结果保留π).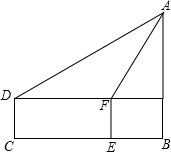 小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.
小丽为了测旗杆AB的高度,小丽眼睛距地面1.5米,小丽站在C点,测出旗杆A的仰角为30°,小丽向前走了10米到达点E,此时的仰角为60°,求旗杆的高度.