题目内容
1.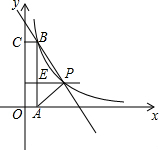 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴,y轴上,函数y=$\frac{k}{x}$的图象过点P(4,3)和矩形的顶点B(m,n)(0<m<4).(1)求k的值;
(2)连接PA,PB,若△ABP的面积为6,求直线BP的解析式.
分析 (1)把P(4,3)代入y=$\frac{k}{x}$,即可求出k的值;
(2)由函数y=$\frac{12}{x}$的图象过点B(m,n),得出mn=12.根据△ABP的面积为6列出方程$\frac{1}{2}$n(4-m)=6,将mn=12代入,化简得4n-12=12,解方程求出n=6,再求出m=2,那么点B(2,6).设直线BP的解析式为y=ax+b,将B(2,6),P(4,3)代入,利用待定系数法即可求出直线BP的解析式.
解答 解:(1)∵函数y=$\frac{k}{x}$的图象过点P(4,3),
∴k=4×3=12;
(2)∵函数y=$\frac{12}{x}$的图象过点B(m,n),
∴mn=12.
∵△ABP的面积为6,P(4,3),0<m<4,
∴$\frac{1}{2}$n(4-m)=6,
∴4n-12=12,
解得n=6,
∴m=2,
∴点B(2,6).
设直线BP的解析式为y=ax+b,
∵B(2,6),P(4,3),
∴$\left\{\begin{array}{l}{2a+b=6}\\{4a+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=-\frac{3}{2}}\\{b=9}\end{array}\right.$,
∴直线BP的解析式为y=-$\frac{3}{2}$x+9.
点评 本题考查了反比例函数与一次函数的交点问题,反比例函数图象上点的坐标特征,待定系数法求一次函数与反比例函数的解析式,三角形的面积,正确求出B点坐标是解题的关键.

练习册系列答案
相关题目
11. 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D,下列四个结论:①EF=BE+CF;
②∠BOC=90°+$\frac{1}{2}$∠A;
③点O到△ABC各边的距离相等;
④设OD=m,AE+AF=n,则S△AEF=mn.
其中正确的结论是( )
| A. | ①②③ | B. | ①②④ | C. | ②③④ | D. | ①③④ |
9.九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
已知该运动服的进价为每件60元,设售价为x元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 (x-60)元;②月销量是 (400-2x)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
(1)请用含x的式子表示:①销售该运动服每件的利润是 (x-60)元;②月销量是 (400-2x)件;(直接写出结果)
(2)设销售该运动服的月利润为y元,那么售价为多少时,当月的利润最大,最大利润是多少?
13.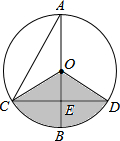 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
 如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )
如图,已知⊙O的一条直径AB与弦CD相交于点E,且AC=2,AE=$\sqrt{3}$,CE=1,则图中阴影部分的面积为( )| A. | $\frac{2\sqrt{3}π}{9}$ | B. | $\frac{4\sqrt{3}π}{9}$ | C. | $\frac{2π}{9}$ | D. | $\frac{4π}{9}$ |
11.化简$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}-{b}^{2}}$-$\frac{b}{a-b}$的结果是( )
| A. | $\frac{a}{a-b}$ | B. | $\frac{b}{a-b}$ | C. | $\frac{a}{a+b}$ | D. | $\frac{b}{a+b}$ |
 如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.
如图,已知直线y=x+k和双曲线y=$\frac{k+1}{x}$(k为正整数)交于A,B两点.
