题目内容
7. 一次函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,则化简:$\sqrt{(n-m)^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为( )
一次函数y=(m-3)x+n-2(m,n为常数)的图象如图所示,则化简:$\sqrt{(n-m)^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为( )| A. | -2n+3 | B. | -2m+3 | C. | m-3 | D. | -1 |
分析 根据图形分析得出m-3>0,n-2<0,然后根据绝对值和二次根式的性质化简即可.
解答 解:由图象可知,m-3>0,n-2<0,
则m>3,n<2,
则:$\sqrt{(n-m)^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|=|n-m|-|n-2|-|m-1|
=m-n-(2-n)-(m-1)
=m-n-2+n-m+1
=-1
故选D.
点评 本题考查了二次根式的性质与化简及一次函数的图象与系数的关系的知识,解答本题的关键是根据图象分析出m、n的取值范围,属于基础题.

练习册系列答案
相关题目

 定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.
定义:如图,点M,N把线段AB分割成三条线段AM,MN和BN,若以AM,MN,BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.若AM=2,MN=3,则BN的长为$\sqrt{3}$或$\sqrt{15}$.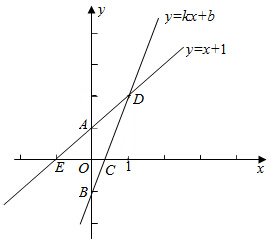 如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0.-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),
如图,已知函数y=x+1的图象与y轴交于点A,一次函数y=kx+b的图象经过点B(0.-1),与x轴以及y=x+1的图象分别交于点C、D,且点D的坐标为(1,n),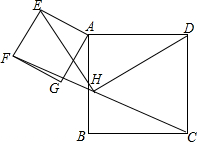 已知,FC是正方形ABCD和正方形AEFG上的点F、C的连线,点H是FC的中点,连接EH、DH,求证:EH=DH,且EH⊥DH.
已知,FC是正方形ABCD和正方形AEFG上的点F、C的连线,点H是FC的中点,连接EH、DH,求证:EH=DH,且EH⊥DH.