题目内容
12．关于x的一元二次方程$\frac{3}{4}$x2-$\sqrt{3}$x+$\sqrt{3}$tanα=0有两个相等的实数根，则锐角α的度数为30°．分析 由方程有两个相等实数根得△=（-$\sqrt{3}$）2-4×$\frac{3}{4}$×$\sqrt{3}$tanα=0，解之可得tanα的值，从而得出锐角α的度数．
解答 解：根据题意得△=（-$\sqrt{3}$）2-4×$\frac{3}{4}$×$\sqrt{3}$tanα=0，
即3-3$\sqrt{3}$tanα=0，
解得：tanα=$\frac{\sqrt{3}}{3}$，
∴锐角α的度数为30°，
故答案为：30°．
点评 本题主要考查一元二次方程根的判别式和特殊锐角的三角函数值，熟练掌握根的判别式的值与方程的根之间的关系是解题的关键．
练习册系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
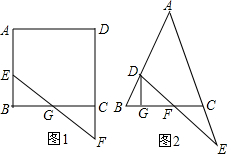（1）如图1，E、F是正方形ABCD的边AB及DC延长线上的点，且BE=CF，则BG与BC的数量关系是BG=$\frac{1}{2}$BC．
7．
一次函数y=（m-3）x+n-2（m，n为常数）的图象如图所示，则化简：$\sqrt{（n-m）^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为（ ）
一次函数y=（m-3）x+n-2（m，n为常数）的图象如图所示，则化简：$\sqrt{（n-m）^{2}}$-$\sqrt{{n}^{2}-4n+4}$-|m-1|的结果为（ ）| A． | -2n+3 | B． | -2m+3 | C． | m-3 | D． | -1 |
如图，△ABC中AB=AC=13，BC=10，点D在边AB上，以D为圆心作⊙D，当⊙D恰好同时与边AC、BC相切时，此时⊙D的半径长为$\frac{120}{23}$．
如图，已知四边形ABCD为⊙O的内接四边形，AE是⊙O的直径，连接BE、BD，P为⊙O外一点，连接PA，若∠AEB=40°，AE=12．