题目内容
如果一条弧长等于
，它的半径是r，那么这条弧所对的圆心角度数为 ，圆心角增加30°时，这条弧长 ．
| πR |
| 4 |
考点：弧长的计算
专题：
分析：根据弧长公式l=
，列出方程求出这条弧所对的圆心角度数；圆心角增加30°时，圆心角为45°+30°=75°，直接代入公式求出即可．
| nπr |
| 180 |
解答：解：设这条弧所对的圆心角度数为n，
依题意有
=
，
解得n=45．
45°+30°=75°，
圆心角增加30°时，这条弧长为
=
．
故答案为：45°，
．
依题意有
| nπr |
| 180 |
| πR |
| 4 |
解得n=45．
45°+30°=75°，
圆心角增加30°时，这条弧长为
| 75×πr |
| 180 |
| 5πr |
| 12 |
故答案为：45°，
| 5πr |
| 12 |
点评：本题主要考查了弧长公式，熟练记忆弧长公式是解题关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
方程（a+2）x2+5xm-3-2=3是关于x的一元一方程，则a和m分别为（ ）
| A、2和4 | B、-2和4 |
| C、-2和-4 | D、-2和-4 |
如图，AB是⊙O的直径，MN是弦，AE⊥MN于E，BF⊥MN于F，AB=10，连EO并延长交BF于S．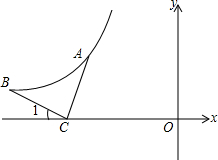
如图，反比例函数y=
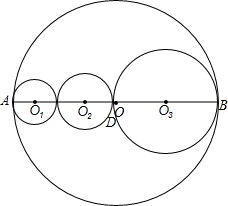如图，点C、D在线段AB上，⊙O、⊙O1、⊙O2、⊙O3的直径分别为AB、AC、CD、DB．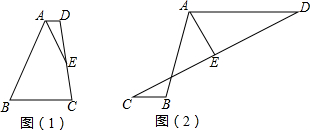
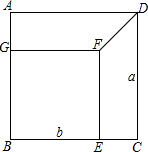如图，将边长为a的正方形ABCD剪去一个边长为b的正方形BEFG，连接DF．根据四边形ABCD，BEFG，AGFD与ECDF的面积关系．你能推出一个什么样的结论？