题目内容
11.已知直线y=2x+1和y=3x+b的交点在第二象限,则b的取值范围是1<b<$\frac{3}{2}$.分析 把y=2x+1和y=3x+b组成方程组,解关于x、y的方程组,求出交点坐标,根据第二象限点的坐标特征解不等式得到答案.
解答 解:由题意得,
$\left\{\begin{array}{l}{y=2x+1}\\{y=3x+b}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=1-b}\\{y=3-2b}\end{array}\right.$,
所以直线y=2x+1和y=3x+b的交点坐标为(1-b,3-2b),
∵交点在第二象限,
∴$\left\{\begin{array}{l}{1-b<0}\\{3-2b>0}\end{array}\right.$,
解得,1<b<$\frac{3}{2}$.
故答案为:1<b<$\frac{3}{2}$.
点评 本题考查的是两条直线相交的问题,正确求出交点、根据题意列出不等式组是解题的关键,注意第二象限点的横坐标小于0,纵坐标大于0.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
2. 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
 将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )
将一个直角三角板和一把直尺如图放置,如果∠α=44°,则∠β的度数是( )| A. | 44° | B. | 45° | C. | 46° | D. | 54° |
19.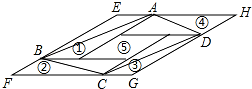 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
 如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.
如图,①②③④⑤五个平行四边形拼成一个含30°内角的菱形EFGH(不重叠无缝隙).若①②③④四个平行四边形面积的和为14cm2,四边形ABCD面积是11cm2,则①②③④四个平行四边形周长的总和为( )cm.| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
6.下列计算正确的是( )
| A. | 2a2-a2=2 | B. | (-a)6÷(-a)2=(-a)3 | C. | (a+b)2=a2+b2 | D. | 2a-1=$\frac{2}{a}$ |
16.某公司根据市场计划调整投资策略,对A,B两种产品进行市场调查,收集数据如表:
其中m是待定常数,其值是由生产A的材料的市场价格决定的,变化范围是6≤m≤8,销售B产品时需缴纳$\frac{1}{20}$x2万元的关税,其中x为生产产品的件数,假定所有产品都能在当年售出,设生产A,B两种产品的年利润分别为y1、y2(万元),写出y1、y2与x之间的函数关系式,注明其自变量x的取值范围.
| 项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
| A | 20 | m | 10 | 200 |
| B | 40 | 8 | 18 | 120 |
20.甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:S${\;}_{甲}^{2}$=2,S${\;}_{乙}^{2}$=1.5,根据以上数据,下列说法正确的是( )
| A. | 甲的成绩比乙的成绩稳定 | B. | 乙的成绩比甲的成绩稳定 | ||
| C. | 甲、乙两人的成绩一样稳定 | D. | 无法确定甲、乙的成绩谁更稳定 |
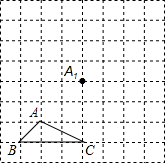 如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).
如图所示,正方形网格中,△ABC为格点三角形(即三角形的顶点都在格点上).