题目内容
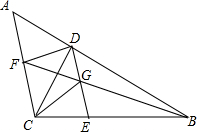 已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.
已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.(1)若∠BGE=∠CGE,求证:∠CEG=2∠CDE;
(2)若DE⊥BC,BE=2CE,FG=FC,探究∠GCE,∠DCG,∠ABF的数量关系.
考点:全等三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)易证∠CGE=∠DGF和CG=FG,即可证明△CGE≌△FGD,可得∠CEG=∠FDG,易证∠CDF=∠CDE,即可求得∠CDE=
∠CEG,即可解题;
(2)根据∠CGE=∠CDE+∠DCG,∠BGE=∠BDE+∠ABF,即可求得∠CGB=∠DCG+∠ABF+90°,易证∠CGB=90°+∠GCE,即可解题.
| 1 |
| 2 |
(2)根据∠CGE=∠CDE+∠DCG,∠BGE=∠BDE+∠ABF,即可求得∠CGB=∠DCG+∠ABF+90°,易证∠CGB=90°+∠GCE,即可解题.
解答:证明:(1)∵DE∥AC,
∴∠CGE=∠ACG,∠BGE=∠BFC,
∵∠CGE=∠BGE,∠BGE=∠DGF,
∴∠ACG=∠BFC,∠CGE=∠DGF,
∴CG=FG,
在△CGE和△FGD中,
,
∴△CGE≌△FGD(SAS),
∴∠CEG=∠FDG,
∵DF是RT△ACD斜边上中线,
∴∠CDF=∠FCD,
∵∠CDE=∠CF,
∴∠CDF=∠CDE,
∴∠CDE=
∠FDG=
∠CEG,
∴2∠CDE=∠CEG;
(2)∵∠CGE=∠CDE+∠DCG,∠BGE=∠BDE+∠ABF,
∴∠CGE+∠BGE=∠CDE+∠DCG+∠BDE+∠ABF,
即∠CGB=∠DCG+∠ABF+∠CDB=∠DCG+∠ABF+90°,①
∵∠CGB+∠CGF=180°,∠GCE+∠FCG=90°,∠FCG=∠CGF,
∴∠CGB=90°+∠GCE,②
由①②得:∠GCE=∠DCG+∠ABF.
∴∠CGE=∠ACG,∠BGE=∠BFC,
∵∠CGE=∠BGE,∠BGE=∠DGF,
∴∠ACG=∠BFC,∠CGE=∠DGF,
∴CG=FG,
在△CGE和△FGD中,
|
∴△CGE≌△FGD(SAS),
∴∠CEG=∠FDG,
∵DF是RT△ACD斜边上中线,
∴∠CDF=∠FCD,
∵∠CDE=∠CF,
∴∠CDF=∠CDE,
∴∠CDE=
| 1 |
| 2 |
| 1 |
| 2 |
∴2∠CDE=∠CEG;
(2)∵∠CGE=∠CDE+∠DCG,∠BGE=∠BDE+∠ABF,
∴∠CGE+∠BGE=∠CDE+∠DCG+∠BDE+∠ABF,
即∠CGB=∠DCG+∠ABF+∠CDB=∠DCG+∠ABF+90°,①
∵∠CGB+∠CGF=180°,∠GCE+∠FCG=90°,∠FCG=∠CGF,
∴∠CGB=90°+∠GCE,②
由①②得:∠GCE=∠DCG+∠ABF.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△CGE≌△FGD是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
2012年国内生产总值为47.2万亿元,数据47.2万亿精确到( )
| A、千亿位 | B、亿位 |
| C、千位 | D、十分位 |
 如图①,在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图②所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为多少?在此你能判定EF与BC的位置关系吗?你观察到相似三角形的基本图形了吗?图②中有几对相似三角形(不包括全等)?
如图①,在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图②所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为多少?在此你能判定EF与BC的位置关系吗?你观察到相似三角形的基本图形了吗?图②中有几对相似三角形(不包括全等)?
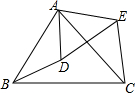 如图,D为△ABC内一点,E为△ABC外一点,且满足
如图,D为△ABC内一点,E为△ABC外一点,且满足 如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标.
如图,在直角坐标系中,矩形ABC0的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.求E点的坐标.