题目内容
 如图①,在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图②所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为多少?在此你能判定EF与BC的位置关系吗?你观察到相似三角形的基本图形了吗?图②中有几对相似三角形(不包括全等)?
如图①,在△ABC中,AB=12,AC=10,BC=9,AD是BC边上的高,将△ABC按如图②所示的方式折叠,使点A与点D重合,折痕为EF,则△DEF的周长为多少?在此你能判定EF与BC的位置关系吗?你观察到相似三角形的基本图形了吗?图②中有几对相似三角形(不包括全等)?考点:相似三角形的判定
专题:
分析:易证AG=DG,根据AD⊥BC即可求得EF∥BC,即可证明△AEF∽△ABC,即可求得△AEF周长,再找出图中所有的相似三角形即可解题.
解答:解:如图,

∵点A与点D重合,
∴AG=DG,即G为AD中点,
∵AD⊥BC,
∴EF∥BC;
∴E为AB中点,F为AC中点,
∴△AEF∽△ABC,且相似比为1:2,
∴C△AEF=
(12+9+10)=15.5;
图②中,△AEF∽△ABC,△AEG∽△ABD,△AFG∽△ACD,△DEG∽△ABD,△DFG∽△ACD.

∵点A与点D重合,
∴AG=DG,即G为AD中点,
∵AD⊥BC,
∴EF∥BC;
∴E为AB中点,F为AC中点,
∴△AEF∽△ABC,且相似比为1:2,
∴C△AEF=
| 1 |
| 2 |
图②中,△AEF∽△ABC,△AEG∽△ABD,△AFG∽△ACD,△DEG∽△ABD,△DFG∽△ACD.
点评:本题考查了相似三角形的判定,考查了相似三角形周长比等于相似比的性质,本题中求证△AEF∽△ABC是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
地球与太阳的平均距离大约为150000000km,这个数据用科学记数法表示正确的是( )
| A、1.5×107 |
| B、1.5×108 |
| C、15×108 |
| D、15×107 |
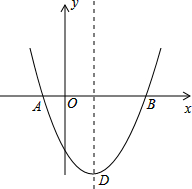 如图,抛物线y=ax2+bx-5交x轴于A(-1,0),B(5,0),顶点为D,交y轴于点C.
如图,抛物线y=ax2+bx-5交x轴于A(-1,0),B(5,0),顶点为D,交y轴于点C.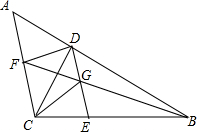 已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.
已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.