题目内容
将一根长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,若设其中一段长为x cm,两个正方形的面积之和为y cm2
(1)写出y与x之间的函数关系式;
(2)当x为何值时,y有最大值,最大值为多少?
(1)写出y与x之间的函数关系式;
(2)当x为何值时,y有最大值,最大值为多少?
考点:二次函数的应用
专题:
分析:(1)由题意可知:设其中一段长为xcm,则另一段长为20-xcm,根据正方形面积和周长的转化关系“正方形的面积=
×周长×周长”列出面积的函数关系式;
(2)由函数的性质求得最值.
| 1 |
| 16 |
(2)由函数的性质求得最值.
解答:解:(1)设一段铁丝的长度为x,另一段为(20-x),则边长分别为
x,
(20-x),
则S=
x2+
(20-x)(20-x)=
(x-10)2+12.5,
(2)S=
(x-10)2+12.5,
所以当x=10cm时,S最小,最小为12.5cm2.
| 1 |
| 4 |
| 1 |
| 4 |
则S=
| 1 |
| 16 |
| 1 |
| 16 |
| 1 |
| 8 |
(2)S=
| 1 |
| 8 |
所以当x=10cm时,S最小,最小为12.5cm2.
点评:本题考查了二次函数的最值,正方形的性质,列出关系式并整理成顶点式形式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在实数-
,
,
,-0.518,
,0.101001…中,无理数的个数有( )
| 21 |
| 7 |
| 8 |
| 3 | -8 |
| π |
| 3 |
| A、2个 | B、3个 | C、4个 | D、5个 |
不等式组
的非负整数解有( )
|
| A、3个 | B、4个 | C、5个 | D、6个 |
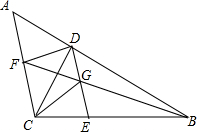 已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.
已知:△ABC中,CD⊥AB于点D,过D作DE∥AC,点G为ED中点,BG的延长线交AC于F,F为AC的中点,连接CG、FD.