题目内容
16．
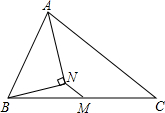如图，在△ABC中，AB=3，AC=7，M为BC的中点，AN平分∠BAC，AN⊥BN，则MN=2．
分析 延长BN交AC于D，易得△ABD是等腰三角形，故可得出AD=AB=3，点N是BD的中点，MN是△BCD的CD边对的中位线，故有MN=$\frac{1}{2}$CD．
解答 
解：如图，延长BN交AC于D．
∵AN⊥BN，AN平分∠BAC，
∴AN是BD的垂直平分线，
∴AD=AB=3，BN=DN
∴点N是BD的中点
∵点M是BC的中点
∴MN是△BCD的中位线
∴MN=$\frac{1}{2}$CD=$\frac{1}{2}$（AC-AD）=2．
故答案是：2．
点评 本题考查了三角形中位线定理和等腰三角形的判定与性质．解题时，需要熟悉等腰三角形的“三线合一”的性质．
练习册系列答案
相关题目
如图，点D、E分别是△ABC边BC、AB上的点，AD、CE相交于点G，过点E作EF∥AD交BC于点F，且CF2=CD•CB，联结FG．
如图，在四边形ABCD中，AC与BD相交于点O，AC=BD，E、F分别是AB、CD的中点，连结EF，分别交AC、BD于点M、N，判断△OMN的形状．