题目内容
12.如图所示,山坡上有一棵与水平面垂直的大树,一场台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面.已知山坡的坡角∠AEF=23°,量得树干倾斜角∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°,AD=6m.(1)求∠CAE的度数;
(2)求这棵大树折断前的高度?
(结果精确到个位,参考数据:$\sqrt{2}$=1.4,$\sqrt{3}$=1.7,$\sqrt{6}$=2.4).

分析 (1)延长BA交EF于点G,根据直角三角形的性质求出∠GAE的度数,再由补角的定义即可得出结论;
(2)过点A作AH⊥CD,垂足为H,在△ADH中,利用锐角三角函数的定义求出DH的长,同理可得出AC的长,由AB=AC+CD即可得出结论.
解答  解:(1)延长BA交EF于点G,在Rt△AGE中,
解:(1)延长BA交EF于点G,在Rt△AGE中,
∵∠E=23°,
∴∠GAE=67°.
又∵∠BAC=38°,
∴∠CAE=180°-67°-38°=75°.
(2)过点A作AH⊥CD,垂足为H.
在△ADH中,
∵∠ADC=60°,AD=6m,
∴DH=AD•cos∠ADC=6cos60°=3,AH=AD•sin∠ADC=6sin60°=3$\sqrt{3}$.
在Rt△ACH中,∠C=180°-75°-60°=45°,
∴CH=AH=3$\sqrt{3}$,
∴AC=$\sqrt{C{H}^{2}+A{H}^{2}}$=$\sqrt{(3\sqrt{3})^{2}+(3\sqrt{3})^{2}}$=$\sqrt{54}$=3$\sqrt{6}$
∴AB=AC+CD=3$\sqrt{6}$+3$\sqrt{3}$+3≈15(米).
答:这棵大树折断前高约15米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,熟记锐角三角函数的定义是解答此题的关键.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒)
某条道路上通行车辆限速为60千米/时,在离道路50米的点P处建一个监测点,道路AB段为检测区(如图).在△ABP中,已知∠PAB=30°,∠PBA=45°,一辆轿车通过AB段的时间8.1秒,请判断该车是否超速?(参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,60千米/时=$\frac{50}{3}$米/秒) 如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
如图,四边形ABCD的对角线AC、BD相交于点O,分别作BE⊥AC于E,DF⊥AC于F,已知OE=OF,CE=AF.
 中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计
中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计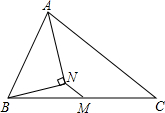 如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2.
如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2.