题目内容
6.(1)计算:($\sqrt{10}$)2+cos60°-$\root{3}{8}$+(3.14-π)0(2)已知关于x的一元二次方程2x2+kx+1=0的一个根为1,求k的值和该方程的另一个根.
分析 (1)将($\sqrt{10}$)2=10、cos60°=$\frac{1}{2}$、$\root{3}{8}$=2以及(3.14-π)0=1代入原式,即可得出结论;
(2)将x=1代入原方程,即可求出k值,设方程的另一个根为m,由根与系数的关系,即可得出1×m=$\frac{1}{2}$,解之即可得出该方程的另一个根.
解答 解:(1)原式=10+$\frac{1}{2}$-2+1=9$\frac{1}{2}$;
(2)将x=1代入原方程,得:2+k+1=0,
解得:k=-3.
设方程的另一个根为m,
由根与系数的关系,得:1×m=$\frac{1}{2}$,
解得:m=$\frac{1}{2}$.
∴k的值为-3,该方程的另一个根为$\frac{1}{2}$.
点评 本题考查了一元二次方程的解、根与系数的关系、零指数幂以及特殊角的三角函数值,解题的关键是:(1)牢记a0=1(a≠0);(2)将x=1代入原方程求出k值.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
14.小东根据学习函数的经验,对函数y=$\frac{4}{(x-1)^{2}+1}$图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{4}{(x-1)^{2}+1}$的自变量x的取值范围是全体实数;
(2)如表是y与x的几组对应值.
表中m的值为$\frac{2}{5}$;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y=$\frac{4}{(x-1)^{2}+1}$的大致图象;

(4)结合函数图象,请写出函数y=$\frac{4}{(x-1)^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)解决问题:如果函数y=$\frac{4}{(x-1)^{2}+1}$与直线y=a的交点有2个,那么a的取值范围是0<a<4.
(1)函数y=$\frac{4}{(x-1)^{2}+1}$的自变量x的取值范围是全体实数;
(2)如表是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{5}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y=$\frac{4}{(x-1)^{2}+1}$的大致图象;

(4)结合函数图象,请写出函数y=$\frac{4}{(x-1)^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)解决问题:如果函数y=$\frac{4}{(x-1)^{2}+1}$与直线y=a的交点有2个,那么a的取值范围是0<a<4.
16.若圆锥的底面半径为3,母线长为5,则这个圆锥的侧面积为( )
| A. | 6π | B. | 8π | C. | 15π | D. | 30π |
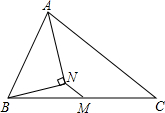 如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2.
如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2. 如图,抛物线y=x2+bx+c经过A(0,2),B(3,2)两点.
如图,抛物线y=x2+bx+c经过A(0,2),B(3,2)两点.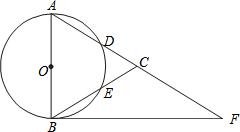 如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.