题目内容
5.因式分解:-2x2y+8xy-6y=-2y(x-1)(x-3).分析 原式提取公因式,再利用十字相乘法分解即可.
解答 解:原式=-2y(x2-4x+3)=-2y(x-1)(x-3),
故答案为:-2y(x-1)(x-3)
点评 此题考查了因式分解-十字相乘法,以及提公因式法,熟练掌握因式分解的方法是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
13. 随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图.
随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图.
根据以上信息回答下列问题:
根据以上信息回答下列问题:
(1)填空:a=0.3,b=24;
(2)请将条形统计图补充完整;
(3)若该市市场上的电动汽车有2000台,请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数.
 随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图.
随着科技的发展,电动汽车的性能得到显著提高,某市对市场上电动汽车的性能进行随机抽样调查,现随机抽取部分电动汽车,记录其一次充电后行驶的里程数,并将抽查数据绘制成如下频数分布直方表和条形统计图.根据以上信息回答下列问题:
| 组别 | 行驶里程x(千米) | 频数(台) | 频率 |
| A | x<200 | 18 | 0.15 |
| B | 200≤x<210 | 36 | a |
| C | 210≤x<220 | 30 | 0.25 |
| D | 220≤x<230 | b | 0.20 |
| E | x≥230 | 12 | 0.10 |
(1)填空:a=0.3,b=24;
(2)请将条形统计图补充完整;
(3)若该市市场上的电动汽车有2000台,请你估计电动汽车一次充电后行驶的里程数在220千米及以上的台数.
14.小东根据学习函数的经验,对函数y=$\frac{4}{(x-1)^{2}+1}$图象与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
(1)函数y=$\frac{4}{(x-1)^{2}+1}$的自变量x的取值范围是全体实数;
(2)如表是y与x的几组对应值.
表中m的值为$\frac{2}{5}$;
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y=$\frac{4}{(x-1)^{2}+1}$的大致图象;

(4)结合函数图象,请写出函数y=$\frac{4}{(x-1)^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)解决问题:如果函数y=$\frac{4}{(x-1)^{2}+1}$与直线y=a的交点有2个,那么a的取值范围是0<a<4.
(1)函数y=$\frac{4}{(x-1)^{2}+1}$的自变量x的取值范围是全体实数;
(2)如表是y与x的几组对应值.
| x | … | -2 | -1 | -$\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | … |
| y | … | $\frac{2}{5}$ | $\frac{4}{5}$ | $\frac{16}{13}$ | 2 | $\frac{16}{5}$ | 4 | $\frac{16}{5}$ | 2 | $\frac{16}{13}$ | $\frac{4}{5}$ | m | … |
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数y=$\frac{4}{(x-1)^{2}+1}$的大致图象;

(4)结合函数图象,请写出函数y=$\frac{4}{(x-1)^{2}+1}$的一条性质:①图象位于一二象限,②当x=1时,函数由值最大4,③当x<1时,y随x的增大而增大,④当x>1时,y随x的增大而减小,⑤图象与x轴没有交点.
(5)解决问题:如果函数y=$\frac{4}{(x-1)^{2}+1}$与直线y=a的交点有2个,那么a的取值范围是0<a<4.
 中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计
中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计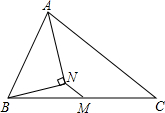 如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2.
如图,在△ABC中,AB=3,AC=7,M为BC的中点,AN平分∠BAC,AN⊥BN,则MN=2. 如图,在?ABCD中,点E是边AD上一点,∠ABE=∠ECB,延长BE交CD的延长线于点F.
如图,在?ABCD中,点E是边AD上一点,∠ABE=∠ECB,延长BE交CD的延长线于点F. 如图,抛物线y=x2+bx+c经过A(0,2),B(3,2)两点.
如图,抛物线y=x2+bx+c经过A(0,2),B(3,2)两点.