题目内容
19. 在平面直角坐标系中,点A、B的坐标分别为(8,0)和(8,4),若点M、N分别是OA、OB上的动点,当AN+MN取最小值时,点N的坐标为($\frac{24}{5}$,$\frac{12}{5}$).
在平面直角坐标系中,点A、B的坐标分别为(8,0)和(8,4),若点M、N分别是OA、OB上的动点,当AN+MN取最小值时,点N的坐标为($\frac{24}{5}$,$\frac{12}{5}$).
分析 作A关于OB的对称点D,过D作DM⊥OA于M,此时AN+MN的值最小,根据三角形面积求出AC,得出AD,证明△ADM∽△BOA求出AM,得出OM,再由平行线的性质得出比例式求出MN即可.
解答 解:作A关于OB的对称点D,过D作DM⊥OA于M交OB于N,如图所示: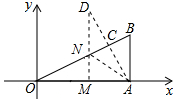
则此时AN+MN=DM的值最小,AD⊥OB,DC=AC,DM∥AB,
∵DN=AN,
∴AN+MN=DN+MN=DM,
∵B(8,4),
∴OB=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
∵△AOB的面积=$\frac{1}{2}$OA•AB=$\frac{1}{2}$OB•AC,
∴AC=$\frac{OA•AB}{OB}$=$\frac{8×4}{4\sqrt{5}}$=$\frac{8\sqrt{5}}{5}$,
∴AD=2AC=$\frac{16\sqrt{5}}{5}$,
∵DM∥AB,
∴∠ADM=∠BAC=∠AOB,
又∵∠AMD=∠BAO=90°,
∴△ADM∽△BOA,
∴$\frac{AM}{BA}=\frac{AD}{OB}$,
即$\frac{AM}{4}=\frac{\frac{16\sqrt{5}}{5}}{4\sqrt{5}}$,
解得:AM=$\frac{16}{5}$,
∴OM=OA-AM=8-$\frac{16}{5}$=$\frac{24}{5}$,
∵DM∥AB,
∴$\frac{MN}{OM}=\frac{AB}{OA}$=$\frac{4}{8}$=$\frac{1}{2}$,
∴MN=$\frac{1}{2}$OM=$\frac{12}{5}$,
∴点N的坐标为($\frac{24}{5}$,$\frac{12}{5}$);
故答案为:($\frac{24}{5}$,$\frac{12}{5}$).
点评 本题考查了轴对称-最短路线问题,勾股定理,三角形相似的判定和性质,关键是求出N点的位置,有一定难度.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | $\frac{x}{y}$=$\frac{3}{4}$ | B. | 3y=4x | C. | $\frac{y+x}{y}$=$\frac{7}{4}$ | D. | $\frac{x}{4}$=$\frac{y}{3}$ |
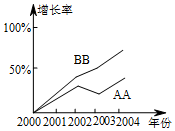 如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”)
如图,是两种品牌的方便面销售增长率折线统计图,则AA牌方便面2003年的销售量低于2002年的销售量,2002年BB牌方便面的销售量高于AA牌方便面的销售量(填“高于”“低于”“不一定高于”) 已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:AE=AB.
已知:如图,在平行四边形ABCD中,点M在边AD上,且AM=DM.CM、BA的延长线相交于点E.求证:AE=AB. 有理数a,b,c在数轴上的位置如图所示,则化简:|a-b|-|c-a|-|b+c|=-2c.
有理数a,b,c在数轴上的位置如图所示,则化简:|a-b|-|c-a|-|b+c|=-2c.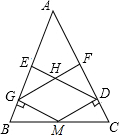 如图,在△ABC中,AB=AC,M为边BC的中点,MG⊥AB,MD⊥AC,DE⊥AB,GF⊥AC,垂足分别为G、D、E、F;GF、DE相交于点H,求证:四边形HGMD是菱形.
如图,在△ABC中,AB=AC,M为边BC的中点,MG⊥AB,MD⊥AC,DE⊥AB,GF⊥AC,垂足分别为G、D、E、F;GF、DE相交于点H,求证:四边形HGMD是菱形.