题目内容
11.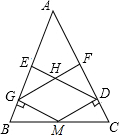 如图,在△ABC中,AB=AC,M为边BC的中点,MG⊥AB,MD⊥AC,DE⊥AB,GF⊥AC,垂足分别为G、D、E、F;GF、DE相交于点H,求证:四边形HGMD是菱形.
如图,在△ABC中,AB=AC,M为边BC的中点,MG⊥AB,MD⊥AC,DE⊥AB,GF⊥AC,垂足分别为G、D、E、F;GF、DE相交于点H,求证:四边形HGMD是菱形.
分析 连接AM,根据同一平面内垂直于同一条直线的两直线互相平行可证明MG∥DE,GF∥DM,进而可得四边形HGMD是平行四边形,再根据等腰三角形三线合一的性质可得AM平分∠BAC,再由角平分线的性质可得MG=MD,进而可得四边形HGMD是菱形.
解答  证明:连接AM,
证明:连接AM,
∵MG⊥AB,DE⊥AB,
∴MG∥DE,
∵MD⊥AC,GF⊥AC,
∴GF∥DM,
∴四边形HGMD是平行四边形,
∵AB=AC,M为边BC的中点,
∴AM平分∠BAC,
∵MG⊥AB,MD⊥AC,
∴MG=MD,
∴四边形HGMD是菱形.
点评 此题主要考查了菱形的判定,关键是掌握一组邻边相等的平行四边形是菱形.

练习册系列答案
相关题目
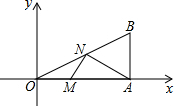 在平面直角坐标系中,点A、B的坐标分别为(8,0)和(8,4),若点M、N分别是OA、OB上的动点,当AN+MN取最小值时,点N的坐标为($\frac{24}{5}$,$\frac{12}{5}$).
在平面直角坐标系中,点A、B的坐标分别为(8,0)和(8,4),若点M、N分别是OA、OB上的动点,当AN+MN取最小值时,点N的坐标为($\frac{24}{5}$,$\frac{12}{5}$).