题目内容
12. AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.
AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.
分析 作OD⊥AC,垂足为D,根据已知可求得OA,AD的长,再根据三角函数求得∠DOA的度数,从而可得到∠AOC的度数.
解答  解:如图,作OD⊥AC,垂足为D
解:如图,作OD⊥AC,垂足为D
∵AB=4
∴OA=2
∵AC=2$\sqrt{3}$,
∴AD=$\sqrt{3}$,
∵sin∠DOA=$\frac{AD}{AO}$=$\frac{\sqrt{3}}{2}$,
∴∠DOA=60°
∴∠AOC=120°.
故答案是:120°.
点评 本题考查了垂径定理和解直角三角形.关键在于根据相关的定理推出AC=2$\sqrt{3}$,然后认真的进行计算.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
20.巡道员沿东西方向的铁路进行巡视维护,他从驻地出发,先向东行走7km,休息之后继续向东行走2km,然后折返向西行走12.5km,用有理数的相关知识回答;此时他在驻地的什么方向?与驻地的距离是多少?
17.将边长为1的正方形纸片如图1所示的方法进行对折,记第一次对折后得到的图形面积为 S1,第2次对折后得到的图形面积为S2…,第n次对折后得到的图形面积为Sn,请根据图2化简S1+S2+S3…S2014=( )
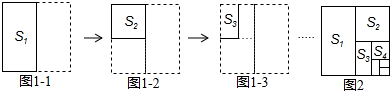

| A. | 1-$\frac{1}{{{2^{2015}}}}$ | B. | $\frac{2014}{2015}$ | C. | 1-$\frac{1}{{{2^{2014}}}}$ | D. | $\frac{2013}{2014}$ |
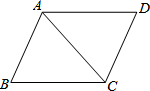 如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.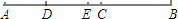 如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.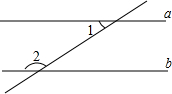 已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.
已知:如图,∠1和∠2是直线a,b被直线c截出的同旁内角,且∠1与∠2互补.求证:a∥b.