题目内容
4.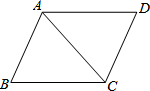 如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
如图,在平行四边形ABCD中,BC=10,sin∠ACB=$\frac{4}{5}$,AC=BC,则平行四边形ABCD的面积是80.
分析 过B作BE垂直于AC,在直角三角形BEC中,利用锐角三角函数定义求出BE的长,求出三角形ABC面积,即可确定出平行四边形ABCD的面积.
解答  解:过B作BE⊥AC,
解:过B作BE⊥AC,
在Rt△BEC中,BC=10,sin∠ACB=$\frac{4}{5}$,
∴BE=BC•sin∠ACB=10×$\frac{4}{5}$=8,
∵AC=BC=10,
∴S△ABC=$\frac{1}{2}$AC•BE=$\frac{1}{2}$×10×8=40,
则平行四边形ABCD的面积为80.
故答案为:80.
点评 此题考查了平行四边形的性质,以及解直角三角形,熟练掌握平行四边形的性质是解本题的关键.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
14.正多边形的一个内角为120°,则该多边形对称轴的条数为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
6.下列图中是四棱柱的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.
AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.
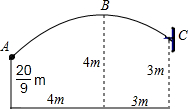 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).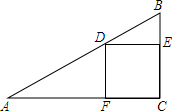 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上. 如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.
如图,在△ABC中,∠ABC=∠ACB,AB的垂直平分线交AC于点M,交AB于点N.连接MB,若AB=8,△MBC的周长是14,则BC的长为6.