题目内容
1.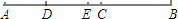 如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=24cm,CB=$\frac{2}{3}$AC,D、E分别为AC、AB的中点,求DE的长.
分析 先求得BC=16cm,从而可求得AB=40cm,然后由中点的定义求得AD=$\frac{1}{2}AC$=12cm,AE=$\frac{1}{2}AB$=20cm,最后由DE=AE-AD求解即可.
解答 解:∵AC=24cm,CB=$\frac{2}{3}$AC,
∴BC=$\frac{2}{3}×24$=16cm.
∴AB=AC+CB=24+16=40cm.
∵D是AC的中点,
∴AD=$\frac{1}{2}AC$=12cm.
∵E是AC的中点,
∴AE=$\frac{1}{2}AB$=20cm.
∴DE=AE-AD=20-12=8cm.
∴DE的长为8cm.
点评 本题主要考查的是两点间的距离,求得AD、AE的长是解题的关键.

练习册系列答案
相关题目
11.下列抛物线中对称轴为过点($\frac{1}{3}$,0)与y轴平行的直线是( )
| A. | $y=\frac{1}{3}{x^2}$ | B. | $y=3{x^2}+\frac{1}{3}$ | C. | $y={({x+\frac{1}{3}})^2}$ | D. | $y={({x-\frac{1}{3}})^2}$ |
6.下列图中是四棱柱的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
4.抛物线y=-2x2+3的顶点在( )
| A. | x轴上 | B. | y轴上 | C. | 第一象限 | D. | 第四象限 |
 AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.
AB是⊙O的直径,AB=4,AC是弦,AC=2$\sqrt{3}$,∠AOC为120°.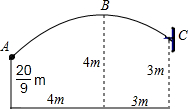 一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).
一场篮球赛中,球员甲跳起投篮,已知球在A处出手时离地面$\frac{20}{9}$m,与篮筐中心C的水平距离为7m,当球运行的水平距离是4m时,达到最大高度4m(B处),篮筐距地面3m,篮球运行的路线为抛物线(如图所示).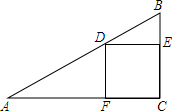 正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.
正方形CEDF的顶点D、E、F分别在△ABC的边AB、BC、AC上.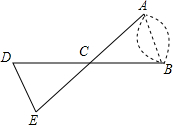 如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理.
如图,A、B两点分别位于一个假山两边,请你利用全等三角形的知识设计一种测量A、B间距离的方案,并说明其中的道理. 如图,截面依次是长方形、三角形、圆形.
如图,截面依次是长方形、三角形、圆形.