题目内容
10.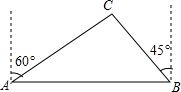 某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由.
某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由.
分析 先过点C作CD⊥AB于D,设CD为xkm,则BD为xkm,AD为$\sqrt{3}$xkm,则有x+$\sqrt{3}$x=2,求出x的值,再与0.7比较大小,即可得出答案.
解答 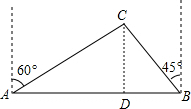 解:如图所示,过点C作CD⊥AB,垂足为点D,
解:如图所示,过点C作CD⊥AB,垂足为点D,
由题意可得:∠CAB=30°,∠CBA=45°,
在Rt△CDB中,∠BCD=45°,
∴∠CBA=∠BCD,∴BD=CD.
在Rt△ACD中,∠CAB=30°,
∴AC=2CD.
设CD=DB=x,
∴AC=2x.
由勾股定理得AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{4{x}^{2}-{x}^{2}}$=$\sqrt{3}$x.
∵AD+DB=2,
∴$\sqrt{3}$x+x=2,
∴x=$\sqrt{3}$-1.
即CD≈0.732>0.7,
答:计划修筑的这条公路不会穿过公园.
点评 此题考查了解直角三角形及勾股定理的应用,用到的知识点是方向角,关键是根据题意画出图形,作出辅助线,构造直角三角形.

练习册系列答案
相关题目
20.若a=$\sqrt{3b-1}$-$\sqrt{1-3b}$+6,则ab的算术平方根是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | ±$\sqrt{2}$ | D. | 4 |
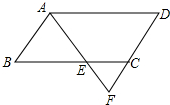 如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度.
如图,在平行四边形ABCD中,E是BC上一点,且AB=BE,AE的延长线交DC的延长线于点F,若∠F=62°,则∠D=56度.