题目内容
18.计算:(1)$\sqrt{8}$×$\sqrt{3}$÷$\sqrt{12}$-$\sqrt{\frac{1}{2}}$
(2)$(4\sqrt{6}-4\sqrt{\frac{1}{2}}+3\sqrt{8})÷2\sqrt{2}$.
分析 (1)根据二次根式的乘除法法则计算;
(2)先把二次根式进行化简,根据二次根式的除法法则计算即可.
解答 解:(1)$\sqrt{8}$×$\sqrt{3}$÷$\sqrt{12}$-$\sqrt{\frac{1}{2}}$=$\sqrt{8×3÷12}$-$\frac{\sqrt{2}}{2}$=$\sqrt{2}$-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$;
(2)$(4\sqrt{6}-4\sqrt{\frac{1}{2}}+3\sqrt{8})÷2\sqrt{2}$=(4$\sqrt{6}$-2$\sqrt{2}$+6$\sqrt{2}$)÷2$\sqrt{2}$=(4$\sqrt{6}$+4$\sqrt{2}$)÷2$\sqrt{2}$=2$\sqrt{3}$+2.
点评 本题考查的是二次根式的混合运算,正确把二次根式根据二次根式的性质进行化简,掌握二次根式的乘法法法则是解题的关键.

练习册系列答案
相关题目
13.如果一元一次不等式组$\left\{\begin{array}{l}{x>3}\\{x≥a}\end{array}\right.$的解集为x>3,则a的取值范围是( )
| A. | a>3 | B. | a≥3 | C. | a<3 | D. | a≤3 |
7.若m>n,下列不等式不一定成立的是( )
| A. | m+2>n+2 | B. | 2m>2n | C. | -2m<-2n | D. | m2>n2 |
8.在-3,-2,2,1四个实数中,最大的实数是( )
| A. | -3 | B. | -2 | C. | 2 | D. | 1 |
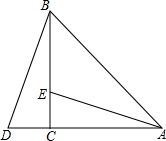 如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,延长AC到点D,使CD=CE.求证: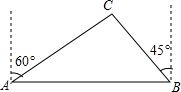 某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由.
某市为方便相距2km的A、B两处居民区的交往,修筑一条笔直的公路(如图:AB),经测量,在A处的北偏东60°方向,B处北偏西45°方向的C处有一半径为0.7km的圆形公园,问计划修筑的公路会不会穿过公园?请说明理由.